题目内容
线段MN上有P、Q两点,MN=32cm,MP=17cm,PQ=6cm.求NQ的长.
解:①若点Q在点P左边,

由题意得:PN=MN-MP=15,
∴NQ=QP+PN=6+15=21;
②若点Q在点P右边,

由题意得:PN=MN-MP=15,
∴NQ=PN-PQ=9.
综上可得NQ的长度为:9cm或21cm.
分析:分两种情况讨论,①点Q在点P左边,②点Q在点P右边,从而可确定NQ的长度.
点评:本题考查求线段长度的知识,有一定难度,关键是讨论P和Q的位置关系.

由题意得:PN=MN-MP=15,
∴NQ=QP+PN=6+15=21;
②若点Q在点P右边,

由题意得:PN=MN-MP=15,
∴NQ=PN-PQ=9.
综上可得NQ的长度为:9cm或21cm.
分析:分两种情况讨论,①点Q在点P左边,②点Q在点P右边,从而可确定NQ的长度.
点评:本题考查求线段长度的知识,有一定难度,关键是讨论P和Q的位置关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某班50名同学分别站在同一公路上相距1000米的M、N两点处,M处有30人,N处有20人,要让两处的同学集合到一起,并且使所有同学走的路程总和最小,那么集合地点应选在
| A.M 点处 | B.N点处 |
| C.线段MN的中点处 | D.线段MN上,距M点400米处 |
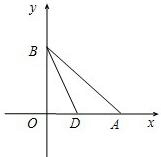 如图平面直角坐标系xoy中,A(1,0)、B(0,1),∠ABO的平分线交x轴于一点D.
如图平面直角坐标系xoy中,A(1,0)、B(0,1),∠ABO的平分线交x轴于一点D.