题目内容
1. 已知:如图OA⊥OB,P是∠AOB内的任意一点,PC⊥OA于点C,PD⊥OB于点D,PC、PD的和为6厘米.求:四边形PCOD的周长.
已知:如图OA⊥OB,P是∠AOB内的任意一点,PC⊥OA于点C,PD⊥OB于点D,PC、PD的和为6厘米.求:四边形PCOD的周长.
分析 先证明四边形PCOD是矩形,得出PC=OD,PD=OC,即可得出四边形PCOD的周长=2(PC+PD)=12厘米.
解答 解:∵OA⊥OB,PC⊥OA,PD⊥OB,
∴∠COD=∠ODP=∠OCP=90°,
∴四边形PCOD是矩形,
∴PC=OD,PD=OC,
∵PC+PD=6厘米,
∴四边形PCOD的周长=2(PC+PD)=12厘米.
点评 本题考查了矩形的判定与性质、菱形周长的计算方法;熟练掌握矩形的判定与性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
11.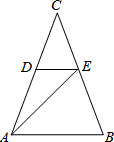 如图,DE∥AB,∠CAE=$\frac{1}{3}$∠CAB,∠CDE=75°,∠B=65°,则∠AEB是( )
如图,DE∥AB,∠CAE=$\frac{1}{3}$∠CAB,∠CDE=75°,∠B=65°,则∠AEB是( )
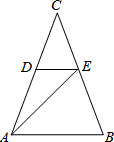 如图,DE∥AB,∠CAE=$\frac{1}{3}$∠CAB,∠CDE=75°,∠B=65°,则∠AEB是( )
如图,DE∥AB,∠CAE=$\frac{1}{3}$∠CAB,∠CDE=75°,∠B=65°,则∠AEB是( )| A. | 70° | B. | 65° | C. | 60° | D. | 55° |
6.已知关于x的方程x2-3x+c=0有一根是x=1,那么这个方程的另一个根是( )
| A. | x=2 | B. | x=-2 | C. | x=-4 | D. | 4 |
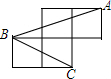 如图,每个小正方形的边长都为1,A、B、C是小正方形的顶点,则∠ABC=45°.
如图,每个小正方形的边长都为1,A、B、C是小正方形的顶点,则∠ABC=45°. 如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.连接AF,BF,则∠ABF的度数是30°.
如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.连接AF,BF,则∠ABF的度数是30°. 某市新建的滴水湖是圆形人工湖.为测量该湖的半径,小杰和小丽沿湖边选取A、B、C三根木柱,使得A、B之间的距离与A、C之间的距离相等,并测得BC长为24米,A到BC的距离为5米,如图所示.请你帮他们求出滴水湖的半径.
某市新建的滴水湖是圆形人工湖.为测量该湖的半径,小杰和小丽沿湖边选取A、B、C三根木柱,使得A、B之间的距离与A、C之间的距离相等,并测得BC长为24米,A到BC的距离为5米,如图所示.请你帮他们求出滴水湖的半径. 如图,DA⊥AC,EB⊥AC,FC⊥AC,AB=2,AC=6,EF=5,那么DF=7.5.
如图,DA⊥AC,EB⊥AC,FC⊥AC,AB=2,AC=6,EF=5,那么DF=7.5.