题目内容
如图,直线 与
与 轴交于
轴交于 ,与
,与 轴交于
轴交于 ,以
,以 为边作矩形
为边作矩形 ,点
,点 在
在 轴上,双曲线
轴上,双曲线 经过点
经过点 与直线
与直线 交于
交于 ,
, 轴于
轴于 ,则
,则 .
.
p;【答案】 解析:
解析:
根据题意,直线y=- x+2与x轴交于C,与y轴交于D,
x+2与x轴交于C,与y轴交于D,
分别令x=0,y=0,
得y=2,x=4,
即D(0,2),C(4,0),
即DC=2 ,
,
又AD⊥DC且过点D,
所以直线AD所在函数解析式为:y=2x+2,
令y=0,得x=-1,
即A(-1,0),
同理可得B点的坐标为B(3,-2)
又B为双曲线y= (k<0)上,
(k<0)上,
代入得k=-6.
即双曲线的解析式为y=
与直线DC联立,
 ,
,
得 和
和
根据题意, 不合题意,
不合题意,
故点E的坐标为(6,-1).
所以BC= ,CE=
,CE= ,
,
CM=2,EM=1,
所以S△BEC= ×BC×EC=
×BC×EC= ,
,
S△EMC= ×EM×CM=1,
×EM×CM=1,
故S四BEMC=S△BEC+S△EMC=
 解析:
解析:根据题意,直线y=-
 x+2与x轴交于C,与y轴交于D,
x+2与x轴交于C,与y轴交于D,分别令x=0,y=0,
得y=2,x=4,
即D(0,2),C(4,0),
即DC=2
 ,
,又AD⊥DC且过点D,
所以直线AD所在函数解析式为:y=2x+2,
令y=0,得x=-1,
即A(-1,0),
同理可得B点的坐标为B(3,-2)
又B为双曲线y=
 (k<0)上,
(k<0)上,代入得k=-6.
即双曲线的解析式为y=

与直线DC联立,
 ,
,得
 和
和
根据题意,
 不合题意,
不合题意,故点E的坐标为(6,-1).
所以BC=
 ,CE=
,CE= ,
,CM=2,EM=1,
所以S△BEC=
 ×BC×EC=
×BC×EC= ,
,S△EMC=
 ×EM×CM=1,
×EM×CM=1,故S四BEMC=S△BEC+S△EMC=


练习册系列答案
相关题目
 ,点
,点
 与
与 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点 .点
.点 在
在 轴上,且
轴上,且 ,在此平面上,存在点
,在此平面上,存在点 ,使得四边形
,使得四边形 恰好为平行四边形.
恰好为平行四边形.
 与
与 轴交于点A,直线
轴交于点A,直线 交于点B,点C在线段AB上,⊙C与
交于点B,点C在线段AB上,⊙C与 轴相切于点P,与OB切于点Q.
轴相切于点P,与OB切于点Q.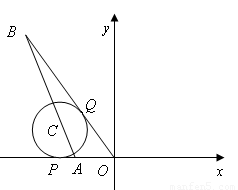
 与
与 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点 .点
.点 在
在 轴上,且
轴上,且 ,在此平面上,存在点
,在此平面上,存在点 ,使得四边形
,使得四边形 恰好为平行四边形.
恰好为平行四边形.
 与
与 轴交于
轴交于 ,与
,与 轴交于
轴交于 ,以
,以 为边作矩形
为边作矩形 ,点
,点 在
在 经过点
经过点 与直线
与直线 ,
, 轴于
轴于 ,则
,则 .
.