题目内容
8.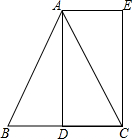 已知:如图,在△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE,垂足为E.
已知:如图,在△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE,垂足为E.(1)求证:△ABD≌△CAE;
(2)连接DE,线段DE与AB之间有怎样的位置和数量关系?请证明你的结论.
分析 (1)运用AAS证明△ABD≌△CAE;
(2)易证四边形ADCE是矩形,所以AC=DE=AB,也可证四边形ABDE是平行四边形得到AB=DE.
解答 证明:(1)∵AB=AC,
∴∠B=∠ACD,
∵AE∥BC,
∴∠EAC=∠ACD,
∴∠B=∠EAC,
∵AD是BC边上的中线,
∴AD⊥BC,
∵CE⊥AE,
∴∠ADC=∠CEA=90°
在△ABD和△CAE中
$\left\{\begin{array}{l}{∠B=∠EAC}\\{∠ADB=∠CEA}\\{AB=CA}\end{array}\right.$
∴△ABD≌△CAE(AAS);
(2)AB=DE,AB∥DE,如右图所示,
∵AD⊥BC,AE∥BC,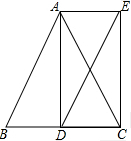
∴AD⊥AE,
又∵CE⊥AE,
∴四边形ADCE是矩形,
∴AC=DE,
∵AB=AC,
∴AB=DE.
∵AB=AC,
∴BD=DC,
∵四边形ADCE是矩形,
∴AE∥CD,AE=DC,
∴AE∥BD,AE=BD,
∴四边形ABDE是平行四边形,
∴AB∥DE且AB=DE.
点评 本题主要考查了三角形全等的判定与性质,矩形的判定与性质以及平行四边形的判定与性质,难度不大,比较灵活.

练习册系列答案
相关题目
16.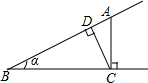 如图,点A为∠α边上的任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是( )
如图,点A为∠α边上的任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是( )
 如图,点A为∠α边上的任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是( )
如图,点A为∠α边上的任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是( )| A. | $\frac{BD}{BC}$ | B. | $\frac{BC}{AB}$ | C. | $\frac{AD}{AC}$ | D. | $\frac{CD}{AC}$ |
9.-5的相反数是( )
| A. | 5 | B. | ±5 | C. | -5 | D. | $\sqrt{5}$ |
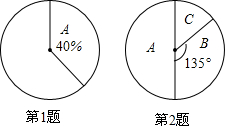 根据扇形统计图,解决下列问题:
根据扇形统计图,解决下列问题: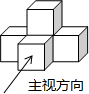 如图是由五个相同的小立方块搭成的几何体,则它的俯视图是( )
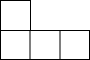
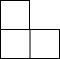
如图是由五个相同的小立方块搭成的几何体,则它的俯视图是( )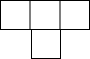
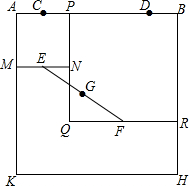 如图,四边形ABHK是边长为6的正方形,点C、D在边AB上,且AC=DB=1,点P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作正方形AMNP和正方形BRQP,E、F分别为MN、QR的中点,连接EF,设EF的中点为G,则当点P从点C运动到点D时,点G移动的路径长为( )
如图,四边形ABHK是边长为6的正方形,点C、D在边AB上,且AC=DB=1,点P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作正方形AMNP和正方形BRQP,E、F分别为MN、QR的中点,连接EF,设EF的中点为G,则当点P从点C运动到点D时,点G移动的路径长为( )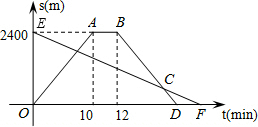 小华从家骑自行车出发,到相距2400米的银行办事,小华出发的同时,他哥哥以匀速的速度从银行沿同一条道路步行回家,小华在银行停留2分钟后沿原路以原速度返回,设他们出发后t分钟时,小华与家之间的距离为S1米,他哥与家之间的距离为S2米,如图中拆线OABD,线段EF分别是表示S1、S2与t之间函数关系的图象.
小华从家骑自行车出发,到相距2400米的银行办事,小华出发的同时,他哥哥以匀速的速度从银行沿同一条道路步行回家,小华在银行停留2分钟后沿原路以原速度返回,设他们出发后t分钟时,小华与家之间的距离为S1米,他哥与家之间的距离为S2米,如图中拆线OABD,线段EF分别是表示S1、S2与t之间函数关系的图象.