题目内容
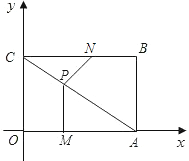
【题目】如图,矩形OABC的顶点A,B的坐标分别为(4,0),(4,3),动点M,N分别从O,B同时出发.以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.过点M作MP⊥OA,交AC于P,连接NP,已知动点运动了![]() 秒.
秒.
(1)当![]() 时,求PC的长;
时,求PC的长;
(2)当![]() 为何值时,△NPC是以PC为腰的等腰三角形?
为何值时,△NPC是以PC为腰的等腰三角形?
【答案】(1)当![]() 时,
时, ![]() ;(2)当
;(2)当![]() 或
或![]() 时,△NPC是以PC为腰的等腰三角形.
时,△NPC是以PC为腰的等腰三角形.
【解析】试题分析:(1)利用平行于三角形底边所构成对应边成比例得到![]() ,代入数据求值.(2)随着M,N点的运动,当PC=PN时, 利用矩形的性质,BC=CN+BN,求得x值 ;当PC=CN时,列出对应边成比例
,代入数据求值.(2)随着M,N点的运动,当PC=PN时, 利用矩形的性质,BC=CN+BN,求得x值 ;当PC=CN时,列出对应边成比例![]() ,代入求值.
,代入求值.
试题解析:
(1)∵ 点A(4,0),B(4,3),∴ OA=4,AB=3,
在矩形OABC中,BC=OA=4,OC=AB=3,∠AOC=∠BCO=90°,
在Rt△AOC中, ![]() ,
,
依题知:OM=BN=![]() =1,又PM⊥OA ,∴ PM∥OC,
=1,又PM⊥OA ,∴ PM∥OC,
∴![]() ,∴
,∴ ![]() ,∴
,∴ ![]() ,
,
∴ 当![]() 时,
时, ![]() .
.
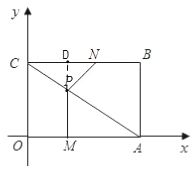
(2)①当PC=PN时,△NPC是以PC为腰的等腰三角形,
延长MP交BC于点为D,
在矩形OABC中,BC∥OA ,∴ PD⊥BC ,
又∠AOC=∠BCO=90°,
∴ 四边形OCDM为矩形 ,∴ CD=OM=![]() ,
,
又PC=PN,PD⊥BC ,∴ CN=2CD=![]() ,
,
∵ BC=CN+BN ,∴ ![]() ,∴
,∴ ![]() ,
,
∴ 当![]() 时,△NPC是以PC为腰的等腰三角形.
时,△NPC是以PC为腰的等腰三角形.
② 当PC=CN时,△NPC是以PC为腰的等腰三角形,
由上面知:CN=BC-BN=![]() =PC, ∵ PM∥OC ,
=PC, ∵ PM∥OC ,
∴![]() , ∴
, ∴![]() , ∴
, ∴![]() ,
,
∴ 当![]() 时,△NPC是以PC为腰的等腰三角形;
时,△NPC是以PC为腰的等腰三角形;
综上所述,当![]() 或
或![]() 时,△NPC是以PC为腰的等腰三角形.
时,△NPC是以PC为腰的等腰三角形.

练习册系列答案
相关题目




