题目内容
如图所示，已知BO平分∠CBA，CO平分∠ACB，MN∥BC，且过点O，若AB=12，AC=14．求△AMN的周长．分析：由BO平分∠CBA，CO平分∠ACB，MN∥BC，易得△OBM与△OCN是等腰三角形，继而可得△AMN的周长等于AB+AC．
解答：解：∵BO平分∠CBA，CO平分∠ACB，
∴∠ABO=∠OBC，∠ACO=∠OCB，
∵MN∥BC，
∴∠MOB=∠OBC，∠NOC=∠OCB，
∴∠ABO=∠MOB，∠ACO=∠NCO，
∴OM=BM，ON=CN，
∵AB=12，AC=14，
∴△AMN的周长：AM+MN+AN=AM+OM+ON+AN=AM+BM+CN+AN=AB+AC=12+14=26．
∴∠ABO=∠OBC，∠ACO=∠OCB，
∵MN∥BC，
∴∠MOB=∠OBC，∠NOC=∠OCB，
∴∠ABO=∠MOB，∠ACO=∠NCO，
∴OM=BM，ON=CN，
∵AB=12，AC=14，
∴△AMN的周长：AM+MN+AN=AM+OM+ON+AN=AM+BM+CN+AN=AB+AC=12+14=26．
点评：此题考查了等腰三角形的性质与判定．此题难度适中，注意掌握数形结合思想的应用．
练习册系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
（1）如图所示，已知OD平分∠AOB，OE平分∠AOC，∠AOB=60°，∠DOE=40°，求∠BOC的度数．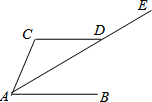
（2013•宜春模拟）如图所示，已知AE平分∠BAC交CD于点D，且AB∥CD，∠C=100°，则∠EAC为（ ）
如图所示，已知BE平分∠ABC，DE∥BC，∠ABC=60°，求∠BED的度数．