��Ŀ����
��ͼ��ij��¥�Ķ�����һ������CD��С����ɽ�µ��½�A����ù���Ƶײ�D������Ϊ60�㣮������AB�����ߵ�B����ù���ƶ���C������Ϊ45�㣬��֪sin��BAH=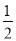 ��AB=10�ף�AE=15�ף�
��AB=10�ף�AE=15�ף�

��1�����B��ˮƽ��AE�ĸ߶�BH��
��2��������CD�ĸ߶ȣ�
��1��5�ף���2�������CD�ĸ߶�Ϊ��20��10���ף� �������������������1���������ҵĸ������BH�ij��� ��2���ڡ�ADE��ֱ�����������DE�ij������������EH��BG�ij�����Rt��CBG�У���CBG=45�㣬��CG=BG���ɴ˿����CG�ij�Ȼ�����CD=CG+GE-DE�����������Ƶĸ߶ȣ� �����������1��������ã�sin��BAH=����AB=10�ף� ��BH= AB...
��ϰ��ϵ�д�
 ��ǰ����ϵ�д�
��ǰ����ϵ�д�
�����Ŀ
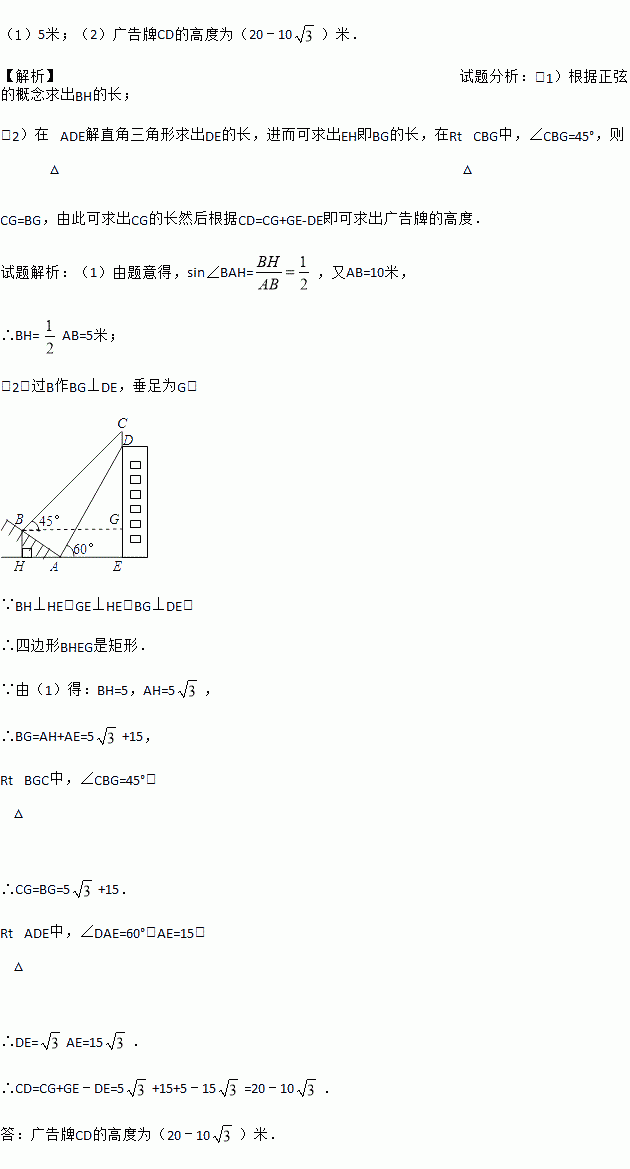

 ����
���� =________��
=________��
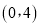 ������������
������������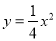 ����A��B���㣬���е�A�ĺ�������-2.
����A��B���㣬���е�A�ĺ�������-2.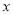 �����Ƿ���ڵ�C,ʹ��?ABC��ֱ�������Σ������ڣ������C�����꣬�������ڣ���˵�����ɣ�
�����Ƿ���ڵ�C,ʹ��?ABC��ֱ�������Σ������ڣ������C�����꣬�������ڣ���˵�����ɣ� 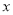 �ᣬ���������ڵ�M,��M�ڵ�һ���ޣ���
�ᣬ���������ڵ�M,��M�ڵ�һ���ޣ���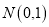 ������M�ĺ�����Ϊ��ֵʱ��MN+3MP�ij���������ֵ�Ƕ��٣�
������M�ĺ�����Ϊ��ֵʱ��MN+3MP�ij���������ֵ�Ƕ��٣�