题目内容
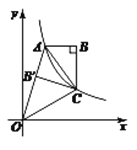
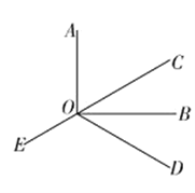
【题目】如图,![]() ,
,![]() 是
是![]() 的平分线,
的平分线,![]() 为
为![]() 的延长线.
的延长线.
(1)当![]() 时,求
时,求![]() 的度数;
的度数;
(2)当![]() 时,求
时,求![]() 的度数;
的度数;
(3)通过(1)(2)的计算,直接写出![]() 和
和![]() 之间的数量关系.
之间的数量关系.
【答案】(1)∠DOE=100°;(2)∠AOC=70°;(3)![]() =2
=2![]()
【解析】
(1)先求出∠BOC,然后根据角平分线的定义即可求出∠COD,最后根据平角的定义即可求出∠DOE;
(2)根据平角的定义先求出∠COD,然后根据角平分线的定义求出∠BOC,即可求出∠AOC;
(3)用∠AOB表示出∠BOC,然后根据角平分线的定义即可求出∠COD,最后根据平角的定义即可求出∠DOE和∠AOC的关系.
解:(1)∵![]() ,
,![]()
∴∠BOC=∠AOB-∠AOC=40°
∵![]() 是
是![]() 的平分线,
的平分线,
∴∠COD=2∠BOC=80°
∴∠DOE=180°-∠COD=100°
(2)∵![]()
∴∠COD=180°-∠DOE=40°
∵![]() 是
是![]() 的平分线,
的平分线,
∴∠BOC=![]() =20°
=20°
∵![]()
∴∠AOC=∠AOB-∠BOC=70°
(3)根据(1)(2)可知:![]() =2
=2![]() ,理由如下
,理由如下
∵![]() ,
,
∴∠BOC=∠AOB-∠AOC=90°-∠AOC
∵![]() 是
是![]() 的平分线,
的平分线,
∴∠COD=2∠BOC=2(90°-∠AOC)=180°-2∠AOC
∴∠DOE=180°-∠COD=180°-(180°-2∠AOC)=2![]() .
.

练习册系列答案
相关题目