题目内容
 在平面直角坐标系中,横、纵坐标都为整数的点叫做整点,设坐标轴的单位为1cm,整点P从原点O出发,速度无1cm/s,且点P只能向上或向右运动,请回答下列问题:
在平面直角坐标系中,横、纵坐标都为整数的点叫做整点,设坐标轴的单位为1cm,整点P从原点O出发,速度无1cm/s,且点P只能向上或向右运动,请回答下列问题:(1)填表:
| 点P从O出发的时间 | 可以到达的整点的坐标 |
| 1秒 | (0,1)、(1,0) |
| 2秒 | (0,2)、(1,1)、(2,0) |
| 3秒 |
(3)当点P从O点出发20秒时,整点P恰好在直线y=2x-4上,求点P的坐标.
考点:一次函数综合题
专题:
分析:(1)根据表中所示的规律,点的横纵坐标的和正好等于时间即可得出第3秒可以到达的整点坐标;
(2)由表中规律可知,横纵坐标的和等于时间,可得,5+10=15秒;
(3)根据横纵坐标的和为20可知,x+y=20,与y=2x-4组成方程组即可解答.
(2)由表中规律可知,横纵坐标的和等于时间,可得,5+10=15秒;
(3)根据横纵坐标的和为20可知,x+y=20,与y=2x-4组成方程组即可解答.
解答:解:(1)∵第1秒可到达的整数点坐标的和:0+1=1,1+0=1;
第2秒可到达的整数点坐标的和:0+2=2,1+1=2,2+0=2;
∴点的横纵坐标的和正好等于时间,
∴第3秒可到达的整数点坐标为:(0,3),(1,2),(2,1),(3,0);
(2)∵由(1)知,点的横纵坐标的和正好等于时间,
∴当到达整点(5,10)时,t=5+10=15秒.
故答案为:15;
(3)设P(x,y),
∵由(1)知,点的横纵坐标的和正好等于时间,
∴
,解得
,
∴P(8,12).
第2秒可到达的整数点坐标的和:0+2=2,1+1=2,2+0=2;
∴点的横纵坐标的和正好等于时间,
∴第3秒可到达的整数点坐标为:(0,3),(1,2),(2,1),(3,0);
(2)∵由(1)知,点的横纵坐标的和正好等于时间,
∴当到达整点(5,10)时,t=5+10=15秒.
故答案为:15;
(3)设P(x,y),
∵由(1)知,点的横纵坐标的和正好等于时间,
∴
|
|
∴P(8,12).
点评:本题考查的是一次函数综合题,根据题意得出点的横纵坐标的和等于时间是解题的关键.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
 如图,半径为5的圆O中,弦AB的长为8,则圆心O到弦AB的距离为( )
如图,半径为5的圆O中,弦AB的长为8,则圆心O到弦AB的距离为( )| A、3 | B、4 | C、5 | D、6 |
实数-2,
,
,-0.3,sin30°,π,0.1010010001,中无理数的个数是( )
| ||
| 2 |
| 22 |
| 7 |
| A、1个 | B、2个. | C、3个 | D、4个 |
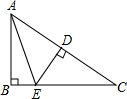 如图,在Rt△ABC中,∠ABC=90°,DE是AC的垂直平分线,交AC于点D,交BC于点E,∠BAE=20°,则∠C的度数是( )
如图,在Rt△ABC中,∠ABC=90°,DE是AC的垂直平分线,交AC于点D,交BC于点E,∠BAE=20°,则∠C的度数是( )| A、30° | B、35° |
| C、40° | D、50° |
在
、1.732、
,、-
四个数中,其中是无理数的是( )
| ||
| 2 |
| 16 |
| 22 |
| 7 |
A、
| ||||
| B、1.732 | ||||
C、
| ||||
D、-
|
