题目内容
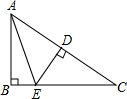如图，在Rt△ABC中，∠ABC=90°，DE是AC的垂直平分线，交AC于点D，交BC于点E，∠BAE=20°，则∠C的度数是（ ）| A、30° | B、35° |
| C、40° | D、50° |
考点：线段垂直平分线的性质
专题：
分析：首先根据线段垂直平分线的性质可得AE=EC，根据等边对等角可得∠C=∠EAC，设∠C=x°，则∠EAC=x°，根据三角形内角和公式可得方程 x+x+20+90=180，再解方程即可．
解答：解：∵DE是AC的垂直平分线，
∴AE=EC，
∴∠C=∠EAC，
设∠C=x°，则∠EAC=x°，
∵∠ABC=90°，∠BAE=20°，
∴x+x+20+90=180，解得：x=35，
∴∠C=35°，
故选：B．
∴AE=EC，
∴∠C=∠EAC，
设∠C=x°，则∠EAC=x°，
∵∠ABC=90°，∠BAE=20°，
∴x+x+20+90=180，解得：x=35，
∴∠C=35°，
故选：B．
点评：此题主要考查了线段的垂直平分线，以及三角形内角和公式，关键是掌握：垂直平分线上任意一点，到线段两端点的距离相等．
练习册系列答案
相关题目
下列调查方式合适差用普查的是（ ）
| A、为了了解全市人民对电影《泰囧》的感受 |
| B、为了了解全校学生每日的运动量 |
| C、为了了解我国公民受教育的情况 |
| D、为了了解某班学生对青岛双星队前NBA巨星麦蒂比赛情况的知晓率 |
计算（m2n）2的结果是（ ）
| A、2m2n |
| B、m4n |
| C、m4n2 |
| D、m2n2 |
在平面直角坐标系中，横、纵坐标都为整数的点叫做整点，设坐标轴的单位为1cm，整点P从原点O出发，速度无1cm/s，且点P只能向上或向右运动，请回答下列问题：
Rt△ABC中，∠C=90°，以BC为直径的⊙O交AB于E，OD⊥BC交⊙O于D，DE交BC于F，点P为CB延长线上的一点，PE延长交AC于G，PE=PF，下列结论：