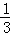题目内容
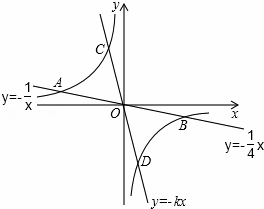
如图,已知双曲线y=﹣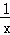 与两直线y=﹣
与两直线y=﹣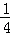 x,y=﹣kx(k>0,且k≠
x,y=﹣kx(k>0,且k≠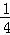 )分别相交于A、B、C、D四点.
)分别相交于A、B、C、D四点.
(1)当点C的坐标为(﹣1,1)时,A、B、D三点坐标分别是A( , ),B( , ),D( , ).
(2)证明:以点A、D、B、C为顶点的四边形是平行四边形.
(3)当k为何值时,▱ADBC是矩形.
考点: 反比例函数综合题;两点间的距离公式;一次函数的应用;平行四边形的判定与性质;矩形的判定.
专题: 综合题.
分析: (1)由C坐标,利用反比例函数的中心对称性确定出D坐标,联立双曲线y=﹣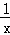 与直线y=﹣
与直线y=﹣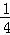 x,求出A与B坐标即可;
x,求出A与B坐标即可;
(2)由反比例函数为中心对称图形,利用中心对称性质得到OA=OB,OC=OD,利用对角线互相平分的四边形为平行四边形即可得证;
(3)由A与B坐标,利用两点间的距离公式求出AB的长,联立双曲线y=﹣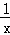 与直线y=﹣kx,表示出CD的长,根据对角线相等的平行四边形为矩形,得到AB=CD,即可求出此时k的值.
与直线y=﹣kx,表示出CD的长,根据对角线相等的平行四边形为矩形,得到AB=CD,即可求出此时k的值.
解答: 解:(1)∵C(﹣1,1),C,D为双曲线y=﹣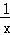 与直线y=﹣kx的两个交点,且双曲线y=﹣
与直线y=﹣kx的两个交点,且双曲线y=﹣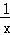 为中心对称图形,
为中心对称图形,
∴D(1,﹣1),
联立得: ,
,
消去y得:﹣ x=﹣
x=﹣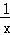 ,即x2=4,
,即x2=4,
解得:x=2或x=﹣2,
当x=2时,y=﹣ ;当x=﹣2时,y=
;当x=﹣2时,y= ,
,
∴A(﹣2, ),B(2,﹣
),B(2,﹣ );
);
故答案为:﹣2, ,2,﹣
,2,﹣ ,1,﹣1;
,1,﹣1;
(2)∵双曲线y=﹣ 为中心对称图形,且双曲线y=﹣
为中心对称图形,且双曲线y=﹣ 与两直线y=﹣
与两直线y=﹣ x,y=﹣kx(k>0,且k≠
x,y=﹣kx(k>0,且k≠ )分别相交于A、B、C、D四点,
)分别相交于A、B、C、D四点,
∴OA=OB,OC=OD,
则以点A、D、B、C为顶点的四边形是平行四边形;
(3)若▱ADBC是矩形,可得AB=CD,
联立得: ,
,
消去y得:﹣ =﹣kx,即x2=
=﹣kx,即x2=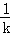 ,
,
解得:x=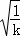 或x=﹣
或x=﹣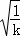 ,
,
当x=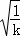 时,y=﹣
时,y=﹣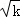 ;当x=﹣
;当x=﹣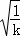 时,y=
时,y=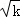 ,
,
∴C(﹣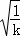 ,
,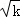 ),D(
),D( ,﹣
,﹣ ),
),
∴CD=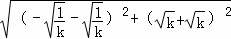 =AB=
=AB= =
=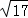 ,
,
整理得:(4k﹣1)(k﹣4)=0,
k1=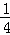 ,k2=4,
,k2=4,
又∵k≠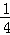 ,∴k=4,
,∴k=4,
则当k=4时,▱ADBC是矩形.
点评: 此题属于反比例函数综合题,涉及的知识有:坐标与图形性质,一次函数与反比例函数的交点,平行四边形,矩形的判定,两点间的距离公式,以及中心图形性质,熟练掌握性质是解本题的关键.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 直线PB为⊙O的切线,
直线PB为⊙O的切线,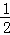 ,求cos∠ADB的值和线段PE的长.
,求cos∠ADB的值和线段PE的长.
 ,再任选一个你喜欢的数x代入求值.
,再任选一个你喜欢的数x代入求值.
 B.
B.  C.
C.  D.
D. 
 相似的是( )
相似的是( )
 B.
B.
 D.
D.
 =k成立,那么k的值为( )
=k成立,那么k的值为( ) A.1 B.-2 C.-2或1 D.以上都不对
A.1 B.-2 C.-2或1 D.以上都不对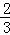 ,12,﹣(﹣96),﹣|﹣3|,﹣4.5,0,|﹣2.5|,
,12,﹣(﹣96),﹣|﹣3|,﹣4.5,0,|﹣2.5|,