题目内容
 如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=5,则四边形CODE的周长是( )
如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=5,则四边形CODE的周长是( )| A、5 | B、7 | C、9 | D、10 |
考点:矩形的性质,菱形的判定与性质
专题:
分析:根据矩形性质求出OC=OD,根据菱形判定得出四边形DECO是菱形,求出OD=OC=EC=DE=
,即可求出答案.
| 5 |
| 2 |
解答:解:∵四边形ABCD是矩形,AC=5,
∴BD=AC=5,AO=OC=
AC=
,BO=OD=
BD=
,
∴DO=OC,
CE∥BD,DE∥AC,
∴四边形DECO是菱形,
∴OD=OC=EC=DE=
,
∴四边形CODE的周长为OD+OC+EC+DE=
+
+
+
=10,
故选D.
∴BD=AC=5,AO=OC=
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
∴DO=OC,
CE∥BD,DE∥AC,
∴四边形DECO是菱形,
∴OD=OC=EC=DE=
| 5 |
| 2 |
∴四边形CODE的周长为OD+OC+EC+DE=
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
故选D.
点评:本题考查了矩形性质和菱形判定和性质的应用,注意:有一组邻边相等的平行四边形是菱形.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
有以下四个命题中,正确的是( )
A、反比例函数y=-
| ||
| B、有一个角相等的两个等腰三角形相似 | ||
| C、抛物线y=x2-2x+2与坐标轴无交点 | ||
| D、垂直于弦的直径平分这条弦,且平分弦所对的弧 |
不解方程,判别2x2-x-1=0的根的情况是( )
| A、方程有两个不相等的实数根 |
| B、方程有两个相等的实数根 |
| C、方程无实数根 |
| D、方程有一个实数根 |
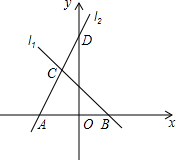 如图,直线l1的解析式为y=-x+2,l1与x轴交于点B,直线l2经过点D(0,5),与直线l1交于点C(-1,m),且与x轴交于点A
如图,直线l1的解析式为y=-x+2,l1与x轴交于点B,直线l2经过点D(0,5),与直线l1交于点C(-1,m),且与x轴交于点A