题目内容
6.已知函数y=kx+b的图象经过(-1,-5)和(1,1)两点,作出函数的图象,并写出函数表达式,回答下列问题:(1)当x取何值时,y≥0?
(2)当y取何值时,x<-1?
(3)当-1≤x<2时,y的取值范围是什么?
分析 先根据待定系数法确定函数解析式,再画出图象.
(1)根据y≥0图象在x轴的上方包括x轴上的点即可写出答案.
(2)根据x<-1,图象上在点(-1,-5)的下方写出答案即可.
(3)当-1≤x<2时,图象上在两点(-1,-5),(2,4)之间包括点(-1,-5)写出答案即可.
解答 解:由题意:$\left\{\begin{array}{l}{-k+b=-5}\\{k+b=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=3}\\{b=-2}\end{array}\right.$,
故函数表达式为y=3x-2.图象如图所示:
由图象可知:(1)当x$≥\frac{2}{3}$时,y≥0.
(2)当y<-5时,x<-1.
(3)当-1≤x<2时,y的取值范围是-5≤y<4.
点评 本题考查一次函数的一个知识,学会待定系数法确定函数解析式,学会根据图象确定自变量或函数值的范围,属于中考常考题型.

练习册系列答案
相关题目
11.在某市中学生田径运动会上,参加男子跳高的15名运动员的成绩如表所示:
这些运动员跳高成绩的中位数是1.53米.
| 成绩(米) | 1.45 | 1.47 | 1.50 | 1.53 | 1.55 | 1.56 |
| 人数 | 1 | 2 | 4 | 3 | 3 | 2 |
18.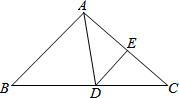 如图,△ABC周长为36cm,把其边AC对折,使点C、A重合,折痕交BC边于点D,交AC边于点E,连结AD,若AE=6cm,则△ABD的周长是( )
如图,△ABC周长为36cm,把其边AC对折,使点C、A重合,折痕交BC边于点D,交AC边于点E,连结AD,若AE=6cm,则△ABD的周长是( )
 如图,△ABC周长为36cm,把其边AC对折,使点C、A重合,折痕交BC边于点D,交AC边于点E,连结AD,若AE=6cm,则△ABD的周长是( )
如图,△ABC周长为36cm,把其边AC对折,使点C、A重合,折痕交BC边于点D,交AC边于点E,连结AD,若AE=6cm,则△ABD的周长是( )| A. | 24cm | B. | 26cm | C. | 28cm | D. | 30cm |
 如图,正方形ABCD,点M在CD上,在AC上确定点N,使DN+MN最小.
如图,正方形ABCD,点M在CD上,在AC上确定点N,使DN+MN最小. 将“富强、民主、文明”六个字分别写在一个正方体的六个面上,正方体的平面展开图如图所示,那么在这个正方体中,和“强”相对的字是( )
将“富强、民主、文明”六个字分别写在一个正方体的六个面上,正方体的平面展开图如图所示,那么在这个正方体中,和“强”相对的字是( ) 王杰为了测量他家小楼附近楼房AB的高度,他从楼底的B处测得到他家小楼顶部D的仰角∠CBD为30°,又测得两幢楼之间的距离BC为10$\sqrt{3}$m.(以下计算结果精确到0.1m,参考值$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{5}$≈2.236)
王杰为了测量他家小楼附近楼房AB的高度,他从楼底的B处测得到他家小楼顶部D的仰角∠CBD为30°,又测得两幢楼之间的距离BC为10$\sqrt{3}$m.(以下计算结果精确到0.1m,参考值$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{5}$≈2.236)