题目内容
 如图,在△ABC中,AD、BE是高,若∠ACB=60°,∠BAC=75°.
如图,在△ABC中,AD、BE是高,若∠ACB=60°,∠BAC=75°.(1)求证:△BDH≌△ADC;
(2)连结DE,求
| DE |
| AB |
考点:全等三角形的判定与性质
专题:计算题
分析:(1)在直角三角形ACD中,由∠ACB的度数求出∠CAD的度数,进而求出∠BAD为45°,得到三角形ABD为等腰直角三角形,即AD=BD,再由一对直角相等,且得到三角形AHE与三角形BHD相似,得到∠CAD=∠HBD,利用ASA即可得证;
(2)连接DE,由AE垂直于BE,AD垂直于BD,得到A、B、D、E四点共圆,利用四边形的外角等于它的内对角得到∠CED=∠ABC,再由公共角,得到三角形CED与三角形ABC相似,由得出得比例,根据直角三角形ACD中,30度所对的直角边等于斜边的一半求出DC与AC之比,即为所求之比.
(2)连接DE,由AE垂直于BE,AD垂直于BD,得到A、B、D、E四点共圆,利用四边形的外角等于它的内对角得到∠CED=∠ABC,再由公共角,得到三角形CED与三角形ABC相似,由得出得比例,根据直角三角形ACD中,30度所对的直角边等于斜边的一半求出DC与AC之比,即为所求之比.
解答: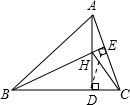 (1)证明:∵∠BDH=∠AEH=90°,∠AHE=∠BHD,
(1)证明:∵∠BDH=∠AEH=90°,∠AHE=∠BHD,
∴△AHE∽△BHD,
∴∠CAD=∠HBD,
∵∠ACB=60°,∠ADC=90°,
∴∠CAD=30°,
∴∠BAD=∠BAC-∠CAD=45°,
∴△ABD为等腰直角三角形,
∴AD=BD,
在△BDH和△ADC中,
,
∴△BDH≌△ADC(ASA);
(2)连接ED,
∵AE⊥BE,AD⊥BD,
∴A、B、D、E四点共圆,
∴∠CED=∠ABC(圆内接四边形外角等于它的内对角),
∵∠ECD=∠BCA,
∴△CED∽△CBA,
∴
=
,
∵∠CAD=30°,
∴在Rt△ACD中,CD=
AC,即
=
,
则
=
.
 (1)证明:∵∠BDH=∠AEH=90°,∠AHE=∠BHD,
(1)证明:∵∠BDH=∠AEH=90°,∠AHE=∠BHD,∴△AHE∽△BHD,
∴∠CAD=∠HBD,
∵∠ACB=60°,∠ADC=90°,
∴∠CAD=30°,
∴∠BAD=∠BAC-∠CAD=45°,
∴△ABD为等腰直角三角形,
∴AD=BD,
在△BDH和△ADC中,
|
∴△BDH≌△ADC(ASA);
(2)连接ED,
∵AE⊥BE,AD⊥BD,
∴A、B、D、E四点共圆,
∴∠CED=∠ABC(圆内接四边形外角等于它的内对角),
∵∠ECD=∠BCA,
∴△CED∽△CBA,
∴
| DE |
| AB |
| CD |
| AC |
∵∠CAD=30°,
∴在Rt△ACD中,CD=
| 1 |
| 2 |
| CD |
| AC |
| 1 |
| 2 |
则
| DE |
| AB |
| 1 |
| 2 |
点评:此题考查了全等三角形的判定与性质,相似三角形的判定与性质,以及等腰直角三角形的性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
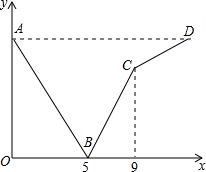 一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,沿同一条道路匀速行驶,设行驶时间为t(h),两车之间的距离为s(km) 图中折线A-B-C-D表示s与t之间的函数关系.试通过计算说明,当快车到达乙地时,慢车还要多少时间才能到达甲地?
一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,沿同一条道路匀速行驶,设行驶时间为t(h),两车之间的距离为s(km) 图中折线A-B-C-D表示s与t之间的函数关系.试通过计算说明,当快车到达乙地时,慢车还要多少时间才能到达甲地? 完成下面推理过程:如图,已知DE∥BC,DF、BE分别平分∠ADE、∠ABC,可推得∠FDE=∠DEB的理由:
完成下面推理过程:如图,已知DE∥BC,DF、BE分别平分∠ADE、∠ABC,可推得∠FDE=∠DEB的理由: