题目内容
19．若x2+$\frac{1}{{x}^{2}}$=7，则x-$\frac{1}{x}$=±$\sqrt{5}$，x+$\frac{1}{x}$=±3．分析 利用完全平方公式化简（x-$\frac{1}{x}$）2与（x+$\frac{1}{x}$）2，将已知等式代入开方即可求出所求式子的值．
解答 解：∵x2+$\frac{1}{{x}^{2}}$=7，
∴（x-$\frac{1}{x}$）2=x2+$\frac{1}{{x}^{2}}$-2=7-2=5，（x+$\frac{1}{x}$）2=x2+$\frac{1}{{x}^{2}}$+2=7+2=9，
∴x-$\frac{1}{x}$=±$\sqrt{5}$，x+$\frac{1}{x}$=±3，
故答案为：±$\sqrt{5}$；±3
点评 此题考查了完全平方公式，熟练掌握完全平方公式是解本题的关键．
练习册系列答案
相关题目
13．
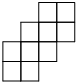将数字2放入图中的10个小方格中，则数字2放在两个“田”字形重叠方格的概率是（ ）
将数字2放入图中的10个小方格中，则数字2放在两个“田”字形重叠方格的概率是（ ）| A． | $\frac{1}{10}$ | B． | $\frac{1}{5}$ | C． | $\frac{3}{10}$ | D． | $\frac{2}{5}$ |