题目内容
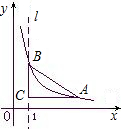
如图,直线l: 经过点M,一组抛物线的顶点B1(1,y),B2(2,y2),B3(3,y3),…,Bn(n,yn)(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1,0),A2(x2,0),A3(x3,0),…
经过点M,一组抛物线的顶点B1(1,y),B2(2,y2),B3(3,y3),…,Bn(n,yn)(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1,0),A2(x2,0),A3(x3,0),… An+1(xn+1,0)(n为正整数),设x1=d(0<d<1).
An+1(xn+1,0)(n为正整数),设x1=d(0<d<1).
(1)求经过点A1、B1、A2的抛物线的解析式(用含d的代数式表示);
(2)若抛物线的顶点与x轴的两个交点构成的三角形是直角三角形,则这种抛物线就称为:“美丽抛物线”,那么当d的大小在0<d<1范围内变化时,这组抛物线中是否存在美丽抛物线?若存在,请求出相应的d的值,若不存在,请说明理由.
解:(1)由题意得:y= x+
x+ ,
,
∵B1(1,y1)在直线l上,
∴当x=1时,y1= ×1+
×1+ =
= ,
,
故可得B1的坐标为(1, ),
),
设抛物线表达式为:y=a(x-1)2+ (a≠0),
(a≠0),
又∵x1=d,
∴A1的坐标为(d,0),
∴0=a(d-1)2+ ,
,
∴a=-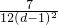 ,
,
∴经过点A1、B1、A2的抛物线的解析式为:y=-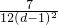 (x-1)2+
(x-1)2+ .
.
(2)存在美丽抛物线.
由(1)可得B1(1, ),B2(1,
),B2(1, ),
),
∵A1(d,0),
∴A2(2-d,0),
①若B1为直角顶点,则A1A2的中点(1,0)到B1的距离与到A1和A2的距离相等,
即:1-d= ,
,
解得:d= ;
;
②若B2为直角顶点,则A2A3的中点(2,0)到B2的距离与到A3和A2的距离相等,
即:2-(2-d)= ,
,
解得:d= ;
;
③若B3为直角顶点,求出的d为负数,并且从B3之后的B点,求出的d都为负数;
综上可得存在d,d的值为 或
或 .
.
分析:(1)把B1(1,y1)代入一次函数式,可求出y1= ,根据图象可知,经过A1、B1、A2的二次函数的顶点就是B1,故其对称轴就是x=1,那么可设函数解析式为:y=a(x-1)2+
,根据图象可知,经过A1、B1、A2的二次函数的顶点就是B1,故其对称轴就是x=1,那么可设函数解析式为:y=a(x-1)2+ 再把A1的坐标代入函数式,可求出a的值,那么就可得到二次函数的解析式;
再把A1的坐标代入函数式,可求出a的值,那么就可得到二次函数的解析式;
(2)根据抛物线的对称性,可知所得直角三角形必是等腰直角三角形,斜边上的高等于斜边的一半,先求出A1、A2、B1、B2…的坐标,若B1为直角顶点,则A1A2的中点(1,0)到B1的距离与到A1和A2的距离相等,求出d的值;同理:若B2为直角顶点,求出d的值;若B3为直角顶点,求出的d值是负数(舍去);总结上述结果即可得出答案.
点评:本题属于二次函数综合题,涉及了二次函数图象上点的坐标特征,直角三角形斜边上的中线等知识点,解此题的关键是进行分类讨论,此题综合性强,难度较大.
 x+
x+ ,
,∵B1(1,y1)在直线l上,
∴当x=1时,y1=
 ×1+
×1+ =
= ,
,故可得B1的坐标为(1,
 ),
),设抛物线表达式为:y=a(x-1)2+
 (a≠0),
(a≠0),又∵x1=d,
∴A1的坐标为(d,0),
∴0=a(d-1)2+
 ,
,∴a=-
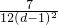 ,
,∴经过点A1、B1、A2的抛物线的解析式为:y=-
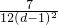 (x-1)2+
(x-1)2+ .
.(2)存在美丽抛物线.
由(1)可得B1(1,
 ),B2(1,
),B2(1, ),
),∵A1(d,0),
∴A2(2-d,0),
①若B1为直角顶点,则A1A2的中点(1,0)到B1的距离与到A1和A2的距离相等,
即:1-d=
 ,
,解得:d=
 ;
;②若B2为直角顶点,则A2A3的中点(2,0)到B2的距离与到A3和A2的距离相等,
即:2-(2-d)=
 ,
,解得:d=
 ;
;③若B3为直角顶点,求出的d为负数,并且从B3之后的B点,求出的d都为负数;
综上可得存在d,d的值为
 或
或 .
.分析:(1)把B1(1,y1)代入一次函数式,可求出y1=
 ,根据图象可知,经过A1、B1、A2的二次函数的顶点就是B1,故其对称轴就是x=1,那么可设函数解析式为:y=a(x-1)2+
,根据图象可知,经过A1、B1、A2的二次函数的顶点就是B1,故其对称轴就是x=1,那么可设函数解析式为:y=a(x-1)2+ 再把A1的坐标代入函数式,可求出a的值,那么就可得到二次函数的解析式;
再把A1的坐标代入函数式,可求出a的值,那么就可得到二次函数的解析式;(2)根据抛物线的对称性,可知所得直角三角形必是等腰直角三角形,斜边上的高等于斜边的一半,先求出A1、A2、B1、B2…的坐标,若B1为直角顶点,则A1A2的中点(1,0)到B1的距离与到A1和A2的距离相等,求出d的值;同理:若B2为直角顶点,求出d的值;若B3为直角顶点,求出的d值是负数(舍去);总结上述结果即可得出答案.
点评:本题属于二次函数综合题,涉及了二次函数图象上点的坐标特征,直角三角形斜边上的中线等知识点,解此题的关键是进行分类讨论,此题综合性强,难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,直线l是经过点(1,0)且与y轴平行的直线.Rt△ABC中直角边AC=4,BC=3.将BC边在直线l上滑动,使A,B在函数
如图,直线l是经过点(1,0)且与y轴平行的直线.Rt△ABC中直角边AC=4,BC=3.将BC边在直线l上滑动,使A,B在函数 14、如图,直线y=kx+b经过点A(-1,-2)和B(-2,0),直线y=2x过点A,则不等式2x<kx+b≤0的解集为
14、如图,直线y=kx+b经过点A(-1,-2)和B(-2,0),直线y=2x过点A,则不等式2x<kx+b≤0的解集为 如图,直线y=kx+b经过点A(-1,3)与x轴交于点
如图,直线y=kx+b经过点A(-1,3)与x轴交于点 15、如图,直线y=kx+b经过点A(-2,0),和B(1,3)两点,则不等式组-2x+5≥kx+b>0的解集为
15、如图,直线y=kx+b经过点A(-2,0),和B(1,3)两点,则不等式组-2x+5≥kx+b>0的解集为 如图,直线y=kx-6经过点A(4,0),且与直线y=-3x+3交于点C.
如图,直线y=kx-6经过点A(4,0),且与直线y=-3x+3交于点C.