Question

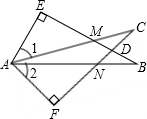如图，∠E=∠F=90°，∠B=∠C，AE=AF．给出下列结论：①∠1=∠2；②BE=CF；③△ACN≌△AMB；④CD=DN．其中正确的结论是（　　）

• A、①②③
• B、①③④
• C、①②
• D、②③

Answer 1

考点：全等三角形的判定与性质

专题：

分析：根据条件∠E=∠F=90°，∠B=∠C，AE=AF可得△ABE≌△ACF，三角形全等的性质BE=CF；∠BAE=∠CAF可得①∠1=∠2；由ASA可得△ACN≌△ABM．④CD=DN不成立．

解答：解：在△ABE和△ACF中，

∠E=∠F ∠B=∠C AE=AF

，
∴△ABE≌△ACF（AAS）
∴∠BAE=∠CAF，AC=AB，BE=CF②
∴∠BAE-∠BAC=∠CAF-∠BAC，
即∠1=∠2．①
在△ACN和△ABM中，

∠BAC=∠BAC AC=AB ∠C=∠B

，
∴△ACN≌△ABM（ASA）③
∴AN=AM，
∴AB-AN=AC-AM，
即BN=CM．
在△CDM和△BDN中，

∠MDC=∠NDB ∠C=∠B CM=BN

，
∴△CDM≌△BDN（AAS）
∴CD=BD
∴题中正确的结论应该是①②③．
故选A．

点评：本题考查了全等三角形的判定和性质的运用，等式的性质的运用，对图中的全等三角形作出正确判断是正确解答本题的关键．