题目内容
列方程解应用题.
为了落实国务院的指示精神,某地方政府出台了一系列“三农“优惠政策,使农民收入大幅度增加.某农户经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=-2x+80.
(1)写出表示利润的代数式.
(2)该产品销售价定位每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种产品的销售价不高于每千克20元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
为了落实国务院的指示精神,某地方政府出台了一系列“三农“优惠政策,使农民收入大幅度增加.某农户经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=-2x+80.
(1)写出表示利润的代数式.
(2)该产品销售价定位每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种产品的销售价不高于每千克20元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
考点:二次函数的应用
专题:
分析:(1)每件利润乘以件数即为每天的总利润;
(2)设每天销售利润为y元,列出二次函数求最值即可;
(3)令利润为150元,列出方程解得即可.
(2)设每天销售利润为y元,列出二次函数求最值即可;
(3)令利润为150元,列出方程解得即可.
解答:解:(1)∵(x-20)(-2x+80)=-2x2+120x-1600,
∴表示利润的代数式为)=-2x2+120x-1600;
(2)设利润为y,
∵y=-2x2+120x-1600
=-2(x2-60x)-1600,
=-2(x-30)2-1600+1800,
=-2(x-30)2+200;
∴当x=30时,销售利润最大,最大利润为200.
(3)由(2)可知,-2(x-30)2+200=150,
解得(x-30)2=25,
x-30=±5,
解得x1=35>30(舍去),x2=25.
∴表示利润的代数式为)=-2x2+120x-1600;
(2)设利润为y,
∵y=-2x2+120x-1600
=-2(x2-60x)-1600,
=-2(x-30)2-1600+1800,
=-2(x-30)2+200;
∴当x=30时,销售利润最大,最大利润为200.
(3)由(2)可知,-2(x-30)2+200=150,
解得(x-30)2=25,
x-30=±5,
解得x1=35>30(舍去),x2=25.
点评:本题考查了二次函数的性质在实际生活中的应用.最大销售利润的问题常利函数的增减性来解答,我们首先要吃透题意,确定变量,建立函数模型,然后结合实际选择最优方案.其中要注意应该在自变量的取值范围内求最大值(或最小值).

练习册系列答案
相关题目
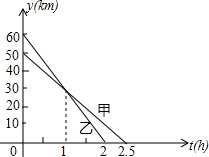 甲、乙两人骑自行车前往A地,他们距A地的路程s(km)与行驶时间t(h)之间的关系如图所示,请根据图象所提供的信息解答下列问题:
甲、乙两人骑自行车前往A地,他们距A地的路程s(km)与行驶时间t(h)之间的关系如图所示,请根据图象所提供的信息解答下列问题: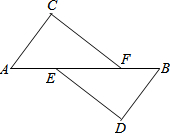 已知,如图:A、E、F、B在一条直线上,AC=BD,∠C=∠D,CF∥DE.
已知,如图:A、E、F、B在一条直线上,AC=BD,∠C=∠D,CF∥DE.