题目内容
12. 如图,AP,CP分别是△ABC外角∠MAC和∠NCA的平分线,它们交于点P.求证:BP为∠MBN的平分线.
如图,AP,CP分别是△ABC外角∠MAC和∠NCA的平分线,它们交于点P.求证:BP为∠MBN的平分线.
分析 利用角平分线性质作垂线得到线段相等,再利用角平分线的逆定理得到所证结果.
解答  证明:过P作三边AB、AC、BC的垂线段PD、PE、PF,
证明:过P作三边AB、AC、BC的垂线段PD、PE、PF,
∵BP是△ABC的外角平分线,PD⊥AD,PF⊥AC,
∴PD=PF(角平分线上的点到角两边的距离相等),
∵CP是△ABC的外角平分线,PE⊥AC,PF⊥BC,
∴PE=PF(角平分线上的点到角两边的距离相等),
∴PD=PE,PD⊥AD,PE⊥AC,
∴AP为∠MBN的平分线(在角的内部,到角两边距离相等的点在角的平分线上).
点评 本题考查角平分线性质,角平分线的性质:角的平分线上的点到角的两边的距离相等.

练习册系列答案
相关题目
20.一个直角三角形的斜边和一条直角边的长分别为17、15,则另一条直角边的长是( )
| A. | 8 | B. | 16 | C. | 10 | D. | 14 |
7.20筐胡萝卜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示. 记录如表:
(1)20筐胡萝卜中,最重的一筐比最轻的一筐重5千克;
(2)与标准重量比较,20筐胡萝卜总计超过或不足多少千克?
(3)若胡萝卜每千克售价2元,则出售这20筐胡萝卜可卖多少元?
| 与标准质量的差值 (单位:千克) | -3 | -2 | -1.5 | 0 | 1 | 2 |
| 筐数 | 1 | 4 | 2 | 4 | 1 | 8 |
(2)与标准重量比较,20筐胡萝卜总计超过或不足多少千克?
(3)若胡萝卜每千克售价2元,则出售这20筐胡萝卜可卖多少元?
4.化简$\sqrt{4}$的结果是( )
| A. | 2 | B. | ±2 | C. | $\sqrt{2}$ | D. | ±$\sqrt{2}$ |
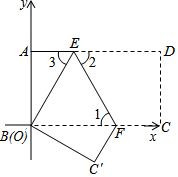 如图.把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置.
如图.把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置.
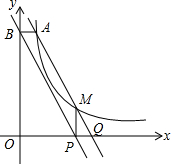 如图,点A(3,2)和点M(m,n)都在反比例函数y=$\frac{k}{x}$(x>0)的图象上.
如图,点A(3,2)和点M(m,n)都在反比例函数y=$\frac{k}{x}$(x>0)的图象上.