题目内容
2．下列运算正确的是（ ）| A． | （x2）3=x5 | B． | （-3x2y）3=-9x6y3 | C． | （a+b）（a+b）=a2+b2 | D． | 4x3y2•（-$\frac{1}{2}$xy2） |
分析 根据整式的运算法则即可求出答案．
解答 解：（A）原式=x6，故A错误；
（B）原式=-27x6y3，故B错误；
（C）原式=a2+2ab+b2，故C错误；
故选（D）
点评 本题考查学生的计算能力，解题的关键是熟练运用整式运算的法则，本题属于基础题型．
练习册系列答案
相关题目
12．计算：（-a）5•（a2）3÷（-a）4的结果，正确的是（ ）
| A． | -a7 | B． | -a6 | C． | a7 | D． | a6 |
13．已知关于x的方程（a-1）x2-2x+1=0有实数根，则a的取值范围是（ ）
| A． | a≤2 | B． | a＞2 | C． | a≤2且a≠1 | D． | a＜-2 |
10．下列说法不正确的是（ ）
| A． | （-$\frac{1}{4}$）2的平方根是±$\frac{1}{4}$ | B． | 0.9的算术平方根是0.3 | ||
| C． | -5是25的一个平方根 | D． | $\root{3}{-27}$=-3 |
17．
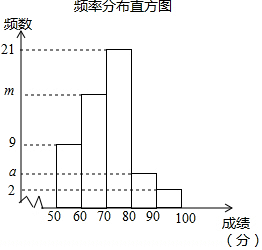为参加学校的“我爱古诗词”知识竞赛，王晓所在班级组织了一次古诗词知识测试，并将全班同学的分数（得分取正整数，满分为100分）进行统计，以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图．请根据以上频率分布表和频率分布直方图，回答下列问题：
（1）求出a、b、m、n的值；
（2）老师说：“王晓的测试成绩是全班同学成绩的中位数”，那么王晓的测试成绩在什么范围内？
（3）若要从小明、小敏等几位成绩优秀（分数在80≤x≤100范围内为优秀）的同学中随机选取两位参加竞赛，请用“列表法”或“树状图”求出小明、小敏同时被选中的概率．（注：几位同学请用A、B、C、D…表示，其中小明为A，小敏为B）
为参加学校的“我爱古诗词”知识竞赛，王晓所在班级组织了一次古诗词知识测试，并将全班同学的分数（得分取正整数，满分为100分）进行统计，以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图．请根据以上频率分布表和频率分布直方图，回答下列问题：| 组别 | 分组 | 频数 | 频率 |
| 1 | 50≤x＜60 | 9 | 0.18 |
| 2 | 60≤x＜70 | a | b |
| 3 | 70≤x＜80 | 21 | 0.42 |
| 4 | 80≤x＜90 | m | 0.06 |
| 5 | 90≤x≤100 | 2 | n |
（2）老师说：“王晓的测试成绩是全班同学成绩的中位数”，那么王晓的测试成绩在什么范围内？
（3）若要从小明、小敏等几位成绩优秀（分数在80≤x≤100范围内为优秀）的同学中随机选取两位参加竞赛，请用“列表法”或“树状图”求出小明、小敏同时被选中的概率．（注：几位同学请用A、B、C、D…表示，其中小明为A，小敏为B）
7．分式$\frac{1}{x-1}$有意义，则x的值为（ ）
| A． | x=1 | B． | x≠0 | C． | x≠1 | D． | x=0 |
11．甲打360个字与乙打480个字所用时间相同，已知两人每分钟共打140个字．若设甲每分钟打x个字，则可列方程（ ）
| A． | $\frac{360}{x}$=$\frac{480}{140-x}$ | B． | $\frac{480}{x}$=$\frac{360}{140-x}$ | C． | $\frac{360}{x}$+$\frac{480}{x}$=140 | D． | x+$\frac{360x}{480}$=140 |