题目内容
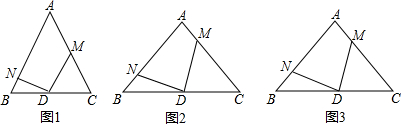
9.如图,在ABC中,AB=AC,点D是BC的中点,M、N分别是AC、AB上的点,且∠A和∠NDM互补.(1)当∠A=60°,如图1,线段BN、MC、AB之间的数量关系是BN+CM=$\frac{1}{2}$AB;
(2)当∠A=90°,如图2,求证:BN+MC=AB;
(3)在(2)的条件下,若CM=3,BN=1,设线段MD交直线AB于点E,求EN的长.
分析 (1)过D作DG∥AB交AC于G,由点D是BC的中点,得到DG=$\frac{1}{2}$AB,∠DGM=60°,证得△BND≌△GMD,根据全等三角形的性质得到BN=GM,即可得到结论;
(2)连接AD,由BD=CD,得到∠DAC=$\frac{1}{2}$∠BAC=∠C=∠BAD=45°,推出△AND≌△CMD,根据全等三角形的性质得到AN=CM,于是得到结论;
(3)连接MN,AD,通过△BDN≌△ADM,由全等三角形的性质得到DN=DM,于是得到△MND是等腰直角三角形,根据勾股定理得到MN=$\sqrt{10}$,可得$DN=DM=\sqrt{5}$,设AE=x,EM=$\sqrt{A{E}^{2}+A{M}^{2}}$=$\sqrt{{x}^{2}+1}$,由勾股定理列方程DN2+DE2=NE2,即可得到结论.
解答 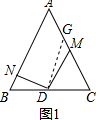 解:(1)BN+CM=$\frac{1}{2}$AB;
解:(1)BN+CM=$\frac{1}{2}$AB;
如图1,过D作DG∥AB交AC于G,
∵点D是BC的中点,
∴DG=$\frac{1}{2}$AB,∠DGM=60°,
∵∠A+∠NDM=180°,
∴∠BND=∠GMD,∠B=∠DGM=60°,BD=DG=$\frac{1}{2}$AB,
在△BND与△GMD中,
$\left\{\begin{array}{l}{∠BND=∠GMD}\\{∠B=∠DGM}\\{BD=DG}\end{array}\right.$,
∴△BND≌△GMD,
∴BN=GM,
∴BN+CM=GM+CM=$\frac{1}{2}$AB;
故答案为:BN+CM=$\frac{1}{2}$AB;
(2)如图2,连接AD,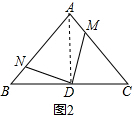
∵BD=CD,
∴∠DAC=$\frac{1}{2}$∠BAC=∠C=∠BAD=45°,
∴AD=CD,
∵∠ADC=90°,∠NDM=90°,
∴∠NDM-∠ADM=∠ADC-∠ADM,
即∠ADN=∠CDM,
在△AND与△CMD中,
$\left\{\begin{array}{l}{∠ADC=∠NDM}\\{∠ADN=∠CDM}\\{AD=CD}\end{array}\right.$,
∴△AND≌△CMD,
∴AN=CM,
∴BN+CM=AB;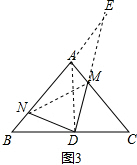
(3)如图3,连接MN,AD,
∴AD=BD=CD,∠BAD=∠B=∠C=45°,∠ADC=∠ADB=90°,
∴∠ADM=∠BDN,
在△BDN与△ADM中,
$\left\{\begin{array}{l}{∠B=∠DAM}\\{BD=AD}\\{∠BDN=∠ADM}\end{array}\right.$,
∴△BDN≌△ADM,
∴DN=DM,
∴△MND是等腰直角三角形,
∵BN=1,CM=3,
∴AN=3,AM=1,
∴MN=$\sqrt{10}$,
∴$DN=DM=\sqrt{5}$,
设AE=x,
∴EM=$\sqrt{A{E}^{2}+A{M}^{2}}$=$\sqrt{{x}^{2}+1}$,
∵DN2+DE2=NE2,即($\sqrt{5}$)2+[$\sqrt{5}$+($\sqrt{{x}^{2}+1}$)]2=(3+x)2,
解得:x=-$\frac{1}{2}$(舍去),x=2,
∴EN=5.
点评 本题考查了全等三角形的判定和性质,等边三角形的性质,等腰直角三角形的性质,勾股定理,正确的作出辅助线是解题的关键.

| A. | 一定小于0 | B. | 可能是0 | C. | 一定大于0 | D. | 一定是有理数 |
| A. | b-a | B. | 3a-b | C. | a+b | D. | 3b-a |
| A. | 对角线相等的四边形是矩形 | |
| B. | 对角线互相垂直的四边形是菱形 | |
| C. | 顺次连接四边形的各边中点所得的四边形是平行四边形 | |
| D. | 两条对角线互相平分且相等的四边形是正方形 |
 如图,AC是△ABC和△ADC的公共边,下列条件中不能判定△ABC≌△ADC的是( )
如图,AC是△ABC和△ADC的公共边,下列条件中不能判定△ABC≌△ADC的是( )| A. | AB=AD,∠2=∠1 | B. | AB=AD,∠3=∠4 | C. | ∠2=∠1,∠3=∠4 | D. | ∠2=∠1,∠B=∠D |
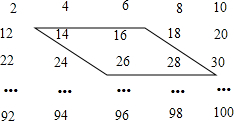 下列数阵是由50个偶数排成的.
下列数阵是由50个偶数排成的.