题目内容

18．若二次函数y=（m+2）x2+mx+m2+5m+6的图象过原点，求m的值．

分析 把原点坐标代入函数解析式可得到关于m的方程，可求得m的值，再根据二次函数的二次函数系数不为零，可求得m的值．

解答 解：
∵二次函数y=（m+2）x2+mx+m2+5m+6的图象过原点，
∴m2+5m+6=0，解得m=-2或m=-3，
∵m+2≠0，
∴m=-3．

点评 本题主要考查二次函数图象上点的坐标特征，掌握函数图象上点的坐标满足函数解析式是解题的关键．

练习册系列答案
相关题目
8．观察下列内容：
$\frac{1}{1×2}$=1-$\frac{1}{2}$，$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$，$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$，$\frac{1}{4×5}$=$\frac{1}{4}$-$\frac{1}{5}$…$\frac{1}{n×（n+1）}$=$\frac{1}{n}-\frac{1}{n+1}$．
请完成下面的问题：
如果有理数a，b满足|ab-2|+（1-b）2=0．
试求$\frac{1}{ab}$+$\frac{1}{（a+1）（b+1）}$+$\frac{1}{（a+2）（b+2）}$+…+$\frac{1}{（a+2016）（b+2016）}$的值．
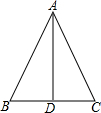9．如图，在△ABC中，AB=AC，AD是BC边上的中线，则∠BDA=90°．
6．用配方法解下列方程：
（1）4x2+4x-3=0
（2）x2+4x-9=2x-11．
13．抛物线y=-3（x-2）2是由抛物线y=-3x2向右平移2个单位得到的，其开口向下，对称轴是x=2，顶点坐标是（2，0）；在对称轴的左边，即x＜0时，曲线自左向右上升，y随x的增大而增大，函数有最大值，即x=2时，有最大值，y=0．
3．一次函数y=mx+8的图象经过一、二、三象限，则m的取值范围是m＞0．
10．比较下列各组数的大小：
（1）$\sqrt{12}$＜$\sqrt{14}$；
（2）$-\sqrt{5}$＞$-\sqrt{7}$；
（3）5＞$\sqrt{24}$；  
（4）$\frac{{\sqrt{24}-1}}{2}$＞1.5．
7．若m，n互为相反数，a，b互为倒数．则m+n+ab+2的值为3．
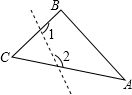8．如图，在△ABC中，∠C=40°，若沿图中虚线剪去∠C，则∠1+∠2=120°．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网