题目内容
15. 如图,一段圆弧过网格的格点A,B,C,若在网格中建立平面直角坐标系,使点A的坐标为(0,-3),点C的坐标为(3,0),则该圆弧所在圆的圆心坐标为( )
如图,一段圆弧过网格的格点A,B,C,若在网格中建立平面直角坐标系,使点A的坐标为(0,-3),点C的坐标为(3,0),则该圆弧所在圆的圆心坐标为( )| A. | (-1,1) | B. | (0,-1) | C. | (1,-1) | D. | (1,0) |
分析 根据垂径定理的推论:弦的垂直平分线必过圆心,可以作弦AB和BC的垂直平分线,交点即为圆心.
解答  解:如图所示,作AC与BC的垂直平分线交于一点O′,
解:如图所示,作AC与BC的垂直平分线交于一点O′,
则O′即为圆弧所在圆的圆心,
∴O′(1,-1).
故选C.
点评 本题考查的是坐标图形性质、垂径定理,熟知“弦的垂直平分线必过圆心”是解答此题的关键.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
11. 如图所示,在菱形ABCD中E是AB的中点,作EF∥BC,交AC于点F,EF=4,那么菱形的周长为( )
如图所示,在菱形ABCD中E是AB的中点,作EF∥BC,交AC于点F,EF=4,那么菱形的周长为( )
 如图所示,在菱形ABCD中E是AB的中点,作EF∥BC,交AC于点F,EF=4,那么菱形的周长为( )
如图所示,在菱形ABCD中E是AB的中点,作EF∥BC,交AC于点F,EF=4,那么菱形的周长为( )| A. | 16 | B. | 30 | C. | 28 | D. | 32 |
3.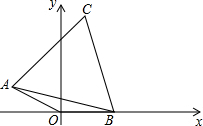 如图,在平面直角坐标系xOy中,点A坐标为(-$\sqrt{3}$,1),连接AO.如果点B是x轴上的一动点,以AB为边作等边三角形ABC.当C(x,y)在第一象限内时,求y与x之间的函数表达式.
如图,在平面直角坐标系xOy中,点A坐标为(-$\sqrt{3}$,1),连接AO.如果点B是x轴上的一动点,以AB为边作等边三角形ABC.当C(x,y)在第一象限内时,求y与x之间的函数表达式.
 如图,在平面直角坐标系xOy中,点A坐标为(-$\sqrt{3}$,1),连接AO.如果点B是x轴上的一动点,以AB为边作等边三角形ABC.当C(x,y)在第一象限内时,求y与x之间的函数表达式.
如图,在平面直角坐标系xOy中,点A坐标为(-$\sqrt{3}$,1),连接AO.如果点B是x轴上的一动点,以AB为边作等边三角形ABC.当C(x,y)在第一象限内时,求y与x之间的函数表达式.
20.将分别标有数字0,1,2,3的司长卡片背面朝上洗匀后,抽取一张作为十位上的数字,再抽取一张作为个位上的数字,每次抽取都不放回,则所得的两位数恰好是奇数的概率等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{5}{9}$ |
4.用配方法解方程2x2-4x+1=0时,配方后所得的方程为( )
| A. | (x-2)2=3 | B. | 2(x-2)2=3 | C. | 2(x-1)2=1 | D. | $2{({x-1})^2}=\frac{1}{2}$ |
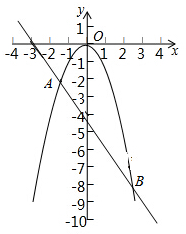 如图所示,抛物线y1=-x2与直线y2=-$\frac{3}{2}x-\frac{9}{2}$交于A,B两点.
如图所示,抛物线y1=-x2与直线y2=-$\frac{3}{2}x-\frac{9}{2}$交于A,B两点.