题目内容
如图，在平面直角坐标系中，四边形ABCD的面积是（ ）| A、4 | ||
B、
| ||
C、
| ||
| D、5 |
考点：坐标与图形性质,三角形的面积
专题：
分析：过点A作AE⊥x轴于E，根据四边形ABCD的面积等于两个直角三角形的面积加上一个梯形的面积，列式计算即可得解．
解答：
解：如图，过点A作AE⊥x轴于E，
则S四边形ABCD=S△COD+S梯形OEAD+S△AEB
=
×1×1+
×（1+2）×2+
×（3-2）×2
=
+3+1
=
．
故选C．
解：如图，过点A作AE⊥x轴于E，则S四边形ABCD=S△COD+S梯形OEAD+S△AEB
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 9 |
| 2 |
故选C．
点评：本题考查了坐标与图形性质，三角形的面积，作辅助线，把不规则四边形分成三个规则图形求解是解题的关键．
练习册系列答案
相关题目
小兰画了一个函数y=x2+ax+b的图象如图，则关于x的方程x2+ax+b=0的解是（ ）| A、无解 | B、x=1 |
| C、x=-4 | D、x=-1或x=4 |
如图1，某超市从一楼到二楼有一自动扶梯，图2是侧面示意图．已知自动扶梯AB的坡度为1：2.4，AB的长度是13米，MN是二楼楼顶，MN∥PQ，C是MN上处在自动扶梯顶端B点正上方的一点，BC⊥MN，在自动扶梯底端A处测得C点的仰角为42°，则二楼的层高BC约为（精确到0.1米，sin42°≈0.67，tan42°≈0.90）（ ）
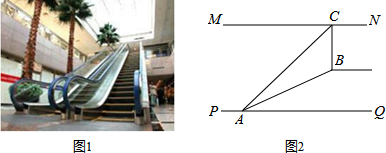
| A、10.8米 | B、8.9米 |
| C、8.0米 | D、5.8米 |
已知a＜b，则下列四个不等式中，不正确的是（ ）
| A、a-2＜b-2 |
| B、a-b＜0 |
| C、2a＞a+b |
| D、-2a＞-2b |
在?ABCD中，∠A：∠B：=2：3，则∠D=（ ）
| A、36° | B、108° |
| C、72° | D、60° |
计算-[-（-a）3]2•（
）-2结果为（ ）
| 1 |
| 3 |
A、
| ||
B、
| ||
| C、-9a6 | ||
D、-
|
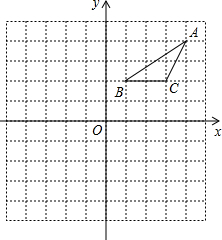在正方形网格中建立如图所示的平面直角坐标系xOy，△ABC的三个顶点都在格点上，点A的坐标是（4，4），请解答下列问题：