题目内容
?ABCD中,E是AD中点,F是AB中点,EF交AC于G,则AG:GC=
- A.1:2
- B.1:3
- C.1:4
- D.1:5
B
分析:连接BD交AC于O,根据平行四边形的性质得出AC=2AO,根据三角形中位线得出EF= BD,EF∥BD,推出
BD,EF∥BD,推出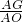 =
= =
= ,得出
,得出 =
= 即可.
即可.
解答:
解:连接BD交AC于O,
∵四边形ABCD是平行四边形,
∴AC=2AO,
∵E、F分别为AD、AB中点,
∴EF= BD,EF∥BD,
BD,EF∥BD,
∴ =
= =
= ,
,
∴ =
= ,
,
∴AG:GC=1:3,
故选B.
点评:本题考查了三角形的中位线,平行四边形的性质的应用,主要考查学生的推理能力.
分析:连接BD交AC于O,根据平行四边形的性质得出AC=2AO,根据三角形中位线得出EF=
 BD,EF∥BD,推出
BD,EF∥BD,推出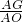 =
= =
= ,得出
,得出 =
= 即可.
即可.解答:

解:连接BD交AC于O,
∵四边形ABCD是平行四边形,
∴AC=2AO,
∵E、F分别为AD、AB中点,
∴EF=
 BD,EF∥BD,
BD,EF∥BD,∴
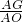 =
= =
= ,
,∴
 =
= ,
,∴AG:GC=1:3,
故选B.
点评:本题考查了三角形的中位线,平行四边形的性质的应用,主要考查学生的推理能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知正方形ABCD中,BD是对角线,BE平分∠DBC交DC于E,若CE=1,则AB长为( )
A、
| ||
B、
| ||
C、
| ||
D、2-
|
 已知:矩形ABCD中,E是CD中点,连接AE并延长交BC延长线于F,M是DF中点,连接CM.
已知:矩形ABCD中,E是CD中点,连接AE并延长交BC延长线于F,M是DF中点,连接CM. 如图,在矩形ABCD中,E是BC的中点,∠BAE=30°,AE=2,则矩形ABCD的面积为
如图,在矩形ABCD中,E是BC的中点,∠BAE=30°,AE=2,则矩形ABCD的面积为