题目内容
三角形三边长a,b,c都是整数,且[a,b,c]=60,(a,b)=4,(b,c)=3(注:[a,b,c]表示a,b,c的最小公倍数,(a,b)表示a,b的最大公约数),则a+b+c的最小值
- A.30
- B.31
- C.32
- D.33
B
分析:首先分解60=3×4×5,得出a,b,c中含的因数有4,3,5,由(a,b)=4,(b,c)=3得出a的最小值是4,b的最小值是3×4,进而得出c的最小值是3×5,从得出a+b+c的最小值.
解答:∵60=2×2×3×5,
∵(a,b)=4,(b,c)=3,
∴a与b是4的倍数,b,c是3的倍数,
∵[a,b,c]=60,
即a,b,c的最小公倍数是60,
∴a,b,c中含的因数有4,3,5,
∴当a=4,b=4×3=12,c=3×5=15时,
a+b+c的最小值是:4+4×3+3×5=31.
故选:B.
点评:此题主要考查了最大公约数与最小公倍数,得出a,b,c的最小值,是解决问题的关键.
分析:首先分解60=3×4×5,得出a,b,c中含的因数有4,3,5,由(a,b)=4,(b,c)=3得出a的最小值是4,b的最小值是3×4,进而得出c的最小值是3×5,从得出a+b+c的最小值.
解答:∵60=2×2×3×5,
∵(a,b)=4,(b,c)=3,
∴a与b是4的倍数,b,c是3的倍数,
∵[a,b,c]=60,
即a,b,c的最小公倍数是60,
∴a,b,c中含的因数有4,3,5,
∴当a=4,b=4×3=12,c=3×5=15时,
a+b+c的最小值是:4+4×3+3×5=31.
故选:B.
点评:此题主要考查了最大公约数与最小公倍数,得出a,b,c的最小值,是解决问题的关键.

练习册系列答案
相关题目
下列能构成直角三角形三边长的是( )
| A、2,3,4 | ||
| B、2,2,3 | ||
C、
| ||
| D、2,6,5 |
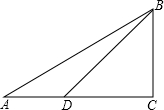 如图,直角三角形三边长AB=10cm,AC=ycm,BC=xcm.
如图,直角三角形三边长AB=10cm,AC=ycm,BC=xcm.