题目内容
.已知菱形ABCD的边长是8,点E在直线AD上,若DE=3,连接BE与对角线AC相交于点M,则 的值是 。
的值是 。
 的值是 。
的值是 。 或
或 如果三角形三边长a,b,c,满足
如果三角形三边长a,b,c,满足 ,那么这个三角形是直角三角形
,那么这个三角形是直角三角形 分析:首先根据题意作图,注意分为E在线段AD上与E在AD的延长线上,然后由菱形的性质可得AD∥BC,则可证得△MAE∽△MCB,根据相似三角形的对应边成比例即可求得答案.

解:∵菱形ABCD的边长是8,
∴AD=BC=8,AD∥BC,
如图1:当E在线段AD上时,
∴AE=AD-DE=8-3=5,
∴△MAE∽△MCB,
∴
 =
= =
= ;
;如图2,当E在AD的延长线上时,
∴AE=AD+DE=8+3=11,
∴△MAE∽△MCB,
∴
 =
= =
= .
.∴
 的值是
的值是 或
或 .
.故答案为:
 或
或 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

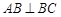 ,
,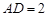 ,
,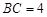 ,点E在AB边上,且CE平分
,点E在AB边上,且CE平分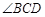 ,DE平分
,DE平分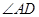 ,则点E到CD的距离为 .
,则点E到CD的距离为 .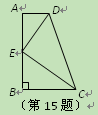
 ㎝2.
㎝2.







