题目内容
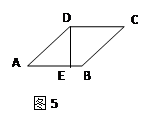
如图,在矩形纸长ABCD中,AD=9,AB=3,将其折叠,使点D与点B重合,折痕为EF,那么DE和EF的长分别为( )


A. | B. | C. | D. |
B
利用直角三角形ABE可求得BE,也就是DE长,构造EF为斜边的直角三角形,进而利用勾股定理求解.
解:连接BD交EF于点O,连接DF.

根据折叠,知BD垂直平分EF.
根据ASA可以证明△DOE≌△BOF,
得OD=OB.
则四边形BEDF是菱形.
设DE=x,则CF=9-x.
在直角三角形DCF中,根据勾股定理,得:x2=(9-x)2+9.
解得:x=5.
在直角三角形BCD中,根据勾股定理,得BD=3 ,则OB=
,则OB=

在直角三角形BOF中,根据勾股定理,得OF= =
= ,则EF=
,则EF= .
.
故选B.
此题主要是能够根据对角线互相垂直平分得菱形DEBF,根据菱形的性质得到边之间的关系,熟练运用勾股定理进行计算.
解:连接BD交EF于点O,连接DF.

根据折叠,知BD垂直平分EF.
根据ASA可以证明△DOE≌△BOF,
得OD=OB.
则四边形BEDF是菱形.
设DE=x,则CF=9-x.
在直角三角形DCF中,根据勾股定理,得:x2=(9-x)2+9.
解得:x=5.
在直角三角形BCD中,根据勾股定理,得BD=3
 ,则OB=
,则OB=

在直角三角形BOF中,根据勾股定理,得OF=
 =
= ,则EF=
,则EF= .
.故选B.
此题主要是能够根据对角线互相垂直平分得菱形DEBF,根据菱形的性质得到边之间的关系,熟练运用勾股定理进行计算.

练习册系列答案
相关题目
 的值是 。
的值是 。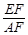 .
.
 cm,求:
cm,求:
 中,
中,
 ,
, ,
, 的垂直平分线交
的垂直平分线交 于
于 ,则
,则 的周长是
的周长是



 处,连结BE.
处,连结BE.
 是菱形;
是菱形; ,则菱形ABCD的周长是________.
,则菱形ABCD的周长是________.