题目内容
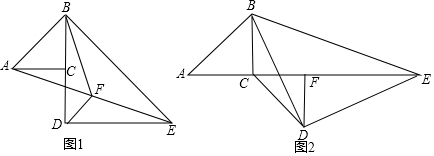
4.如图,△ABC和△BDE都是等腰直角三角形,其中∠ACB=∠BDE=90°,AC=BC,BD=ED,连接AE,点F是AE的中点,连接DF.(1)如图1,若B、C、D共线,且AC=CD=2,求BF的长度;
(2)如图2,若A、C、F、E共线,连接CD,求证:DC=$\sqrt{2}$DF.
分析 (1)证明△ABE是直角三角形,求出AB、BE,理由勾股定理求出AE,再利用直角三角形斜边中线的性质即可解决问题.
(2)作AM∥DE交DF的延长线于M,交BD于N,连接CM.只要证明△CDM,△CDF都是等腰直角三角形即可解决问题;
解答 解:(1)∵△ABC和△BDE都是等腰直角三角形,
∴AC=BC=CD=2,BD=DE=4,BE=4$\sqrt{2}$,AB=2$\sqrt{2}$,∠ABC=∠DBE=45°,
∴∠ABE=90°,
∴AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=$\sqrt{(2\sqrt{2})^{2}+(4\sqrt{2})^{2}}$=2$\sqrt{10}$,
∵AF=EF,
∴BF=$\frac{1}{2}$AE=$\sqrt{10}$.
(2)作AM∥DE交DF的延长线于M,交BD于N,连接CM.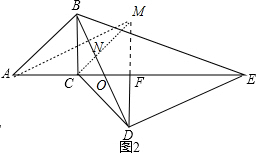
∵AM∥DE,
∴∠MAE=∠DEF,
在△AFM和△EFD中,
$\left\{\begin{array}{l}{∠MAF=∠DEF}\\{AF=EF}\\{∠AFM=∠EFD}\end{array}\right.$,
∴△AFM≌△EFD,
∴AM=DE=BD,
∵∠BCE=∠BDE=90°,∠COB=∠DOE,
∴∠CBD=∠DEF=∠MAF.
在△ACM和△BCD中,
$\left\{\begin{array}{l}{AC=BC}\\{∠MAC=∠CBD}\\{AM=BD}\end{array}\right.$,
∴△ACM≌△BCD,
∴∠ACM=∠BCD,CM=CD,
∴∠ACB=∠MCD=90°
∴△CDM是等腰直角三角形,
易知△BOC∽△EOD,
∴$\frac{OB}{EO}$=$\frac{CO}{OD}$,
∴$\frac{OB}{CO}$=$\frac{OE}{OD}$,
∴△BOE∽△COD,
∴∠DCO=∠OBE=45°,
∴∠FCD=∠FCM=45°,∵CM=CD,
∴FM=DF,CF⊥DM,
∴△CDF是等腰直角三角形,
∴CD=$\sqrt{2}$DF.
点评 本题考查全等三角形的判定和性质、相似三角形的判定和性质、等腰直角三角形的性质、直角三角形斜边中线的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案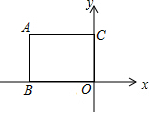 如图,以长方形OCAB的顶点O为原点建立直角坐标系,点B、C分别在x、y轴上,若OB=5,OC=3,则点A可以表示为( )
如图,以长方形OCAB的顶点O为原点建立直角坐标系,点B、C分别在x、y轴上,若OB=5,OC=3,则点A可以表示为( )| A. | (-5,3) | B. | (5,-3) | C. | (-3,5) | D. | (3,-5) |
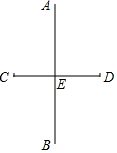 如图,直线AB是线段CD的垂直平分线,则下列结论正确的有( )
如图,直线AB是线段CD的垂直平分线,则下列结论正确的有( )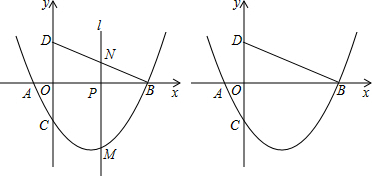
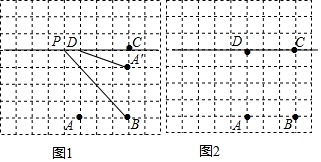
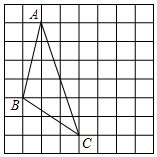 在如图所示的单位正方形网格中
在如图所示的单位正方形网格中