题目内容
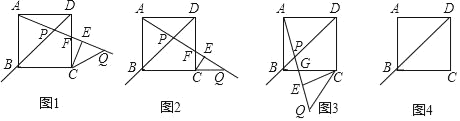
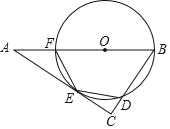
【题目】某仓储中心有一个坡度为i＝1：2的斜坡AB，顶部A处的高AC为4米，B、C在同一水平地面上，其横截面如图．
（1）求该斜坡的坡面AB的长度；
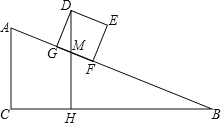
（2）现有一个侧面图为矩形DEFG的长方体货柜，其中长DE＝2.5米，高EF＝2米，该货柜沿斜坡向下时，点D离BC所在水平面的高度不断变化，求当BF＝3.5米时，点D离BC所在水平面的高度DH．
【答案】（1）
米；（2）
m．
【解析】
（1）根据坡度定义以及勾股定理解答即可；
（2）证出∠GDM＝∠HBM，根据
，得到GM＝1m，利用勾股定理求出DM的长，然后求出BM＝5m，进而求出MH，然后得到DH．
（1）∵坡度为i＝1：2，AC＝4m，
∴BC＝4×2＝8m．
∴AB＝
＝
＝（米）；
（2）∵∠DGM＝∠BHM，∠DMG＝∠BMH，
∴∠GDM＝∠HBM，
∴，
∵DG＝EF＝2m，
∴GM＝1m，
∴DM＝
，BM＝BF+FM＝3.5+（2.5﹣1）＝5m，
设MH＝xm，则BH＝2xm，
∴x2+（2x）2＝52，
∴x＝
m，
∴DH＝
＝m．
【题目】某区在实施居民用水管理前，随机调查了部分家庭（单位：户）去年的月均用水量（单位：t），并将调查数据进行整理，绘制出如下不完整的统计图表：
月均用水量 | 频数 | 频率 |
0≤x＜5 | 6 | 12% |
5≤x＜10 | 12 | 24% |
10≤x＜15 |
| 32% |
15≤x＜20 | 10 | 20% |
20≤x＜25 | 4 |
|
25≤x＜30 | 2 | 4% |
合计 |
| 100% |
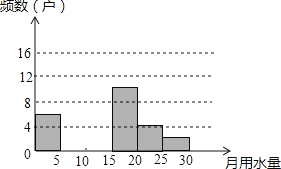
请解答以下问题：
（I）把上面的频数分布表和频数分布直方图补充完整；
（Ⅱ）若该小区有2000户家庭，根据此次随机抽查的数据估计，该小区月均用水量不低于20t的家庭有多少户？
（Ⅲ）为了鼓励节约用水，要确定一个月均用水量的标准，超出该标准的部分按1.5倍价格收费，若要使68%的家庭水费支出不受影响，那么，你觉得家庭月均用水量应定为多少？
