题目内容
13.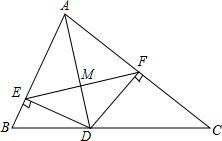 如图,AD是△BAC的平分线,DE⊥AB于E,DF⊥AC于F.
如图,AD是△BAC的平分线,DE⊥AB于E,DF⊥AC于F.(1)求证:DE=DF;
(2)求证:AD垂直平分EF.
分析 (1)由角平分线的性质可证得DE=DF;
(2)由DE=DF,结合条件可证明△AED≌△AFD,可知点A、D都在线段EF的垂直平分线上,可证得结论.
解答 证明:
(1)∵AD是△BAC的平分线,DE⊥AB于E,DF⊥AC于F,
∴DE=DF;
(2)∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°,
在Rt△AED和Rt△AFD中
$\left\{\begin{array}{l}{AD=AD}\\{DE=DF}\end{array}\right.$
∴Rt△AED≌Rt△AFD(HL),
∴AE=AF,
∴点A、D都在线段EF的垂直平分线上,
∴AD垂直平分EF.
点评 本题主要考查角平分线的性质和线段垂直平分线的判定,掌握角平分线上的点到角两边的距离相等是解题的关键.

练习册系列答案
相关题目
18.已知x=-1是一元二次方程x2+mx+n=0的一个根,则(m-n)2的值为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
5. 如图,在梯形ABCD中,AD∥BC,AC⊥AB,AD=CD,cos∠ACD=$\frac{4}{5}$,BC=10,则AB的长为( )
如图,在梯形ABCD中,AD∥BC,AC⊥AB,AD=CD,cos∠ACD=$\frac{4}{5}$,BC=10,则AB的长为( )
 如图,在梯形ABCD中,AD∥BC,AC⊥AB,AD=CD,cos∠ACD=$\frac{4}{5}$,BC=10,则AB的长为( )
如图,在梯形ABCD中,AD∥BC,AC⊥AB,AD=CD,cos∠ACD=$\frac{4}{5}$,BC=10,则AB的长为( )| A. | 5 | B. | 6 | C. | 8 | D. | 5$\sqrt{3}$ |
 如图,点A1,B,C,A2在同一直线上,OM是线段AA1的中垂线,ON是线段AA2的中垂线.若A1A2=6cm,求△ABC的周长.
如图,点A1,B,C,A2在同一直线上,OM是线段AA1的中垂线,ON是线段AA2的中垂线.若A1A2=6cm,求△ABC的周长.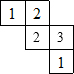 由一些大小相同的小正方体搭成的几何体的俯视图如图所示,其正方形中的数字表示该位置上的小正方体的个数,画出该几何体的主视图.
由一些大小相同的小正方体搭成的几何体的俯视图如图所示,其正方形中的数字表示该位置上的小正方体的个数,画出该几何体的主视图.