题目内容
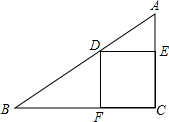在Rt△ABC中，四边形DECF为正方形，若AD=5，DB=6，则△ADE与△BDF的面积之和为________．
15
分析：证明△ADE∽△DFB，得到这两个三角形边之间的关系，再利用DE=DF和勾股定理可求出它们的面积和．
解答：设DE=DF=x．
∵DE∥BF，
∴∠ADE=∠B，
∴△AED∽△DFB，
∴AE：DF=AD：DB=DE：BF，即AE：x=5：6=x：BF，
∴AE=
x，BF=
x，
∴S△AED+S△DFB=
•AE•DE+•BF•DF=
x2，
在Rt△AED中，x2+（x）2=52，
∴x2=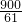
，
∴S△AED+S△DFB=×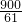=15，
故答案为15．
点评：本题考查了相似三角形的判定与性质：平行于三角形一边的直线与三角形其它两边相角，所截得的三角形与原三角形相似．也考查了正方形的性质和勾股定理
分析：证明△ADE∽△DFB，得到这两个三角形边之间的关系，再利用DE=DF和勾股定理可求出它们的面积和．
解答：设DE=DF=x．
∵DE∥BF，
∴∠ADE=∠B，
∴△AED∽△DFB，
∴AE：DF=AD：DB=DE：BF，即AE：x=5：6=x：BF，
∴AE=
x，BF=x，∴S△AED+S△DFB=
•AE•DE+•BF•DF=x2，在Rt△AED中，x2+（
x）2=52，∴x2=
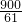，∴S△AED+S△DFB=
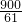×=15，故答案为15．
点评：本题考查了相似三角形的判定与性质：平行于三角形一边的直线与三角形其它两边相角，所截得的三角形与原三角形相似．也考查了正方形的性质和勾股定理
练习册系列答案
小题狂做系列答案
相关题目
如图1，△ABC是直角三角形，如果用四张与△ABC全等的三角形纸片恰好拼成一个等腰梯形，如图2，那么在Rt△ABC中，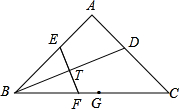
如图，在Rt△ABC中，∠A=90°，AB=AC，∠ABC的平分线BD交AC于点D，BD的垂直平分线分别与AB，BC交于点E，F，在线段BC上取一点G，使CG=CD．
如图，在Rt△ABC中，∠ACB=90゜，正方形EFGH四个顶点分别在三边上，连CH，CG交EF于M、N，求证：EM•FN=MN2．
我们发现，用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题，这种方法称为等面积法，这是一种重要的数学方法．请你用等面积法来探究下列两个问题：