题目内容
如图所示，已知在矩形ABCD中，AB=5，AD=20，点M分BC为BM：MC=1：2，DE⊥AM于点E，求DE的长．考点：相似三角形的判定与性质,勾股定理
专题：
分析：由条件可证明△AED∽△MBA，可得
=
，又由条件可求得AM，代入可求得DE．
| DE |
| AB |
| AD |
| AM |
解答：解：∵四边形ABCD为矩形，
∴AD∥BC，
∴∠DAE=∠AMB，
∵AE⊥DE，
∴∠DEA=∠B，
∴△AED∽△MBA，
∴
=
，
∵BM：MC=1：2，BC=AD=20，
∴BM=
，且AB=5，
∴AM=
，
∴
=
，
解得DE=12．
∴AD∥BC，
∴∠DAE=∠AMB，
∵AE⊥DE，
∴∠DEA=∠B，
∴△AED∽△MBA，
∴
| DE |
| AB |
| AD |
| AM |
∵BM：MC=1：2，BC=AD=20，
∴BM=
| 20 |
| 3 |
∴AM=
| 25 |
| 3 |
∴
| DE |
| 5 |
| 20 | ||
|
解得DE=12．
点评：本题主要考查相似三角形的判定和性质，解得AM的长是解题的关键，注意比例的应用．
练习册系列答案
相关题目
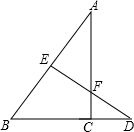已知，CA⊥DB，DE⊥AB，AC、ED交于F，BC=3，FC=1，BD=5，则AC=
如图，∠AOB=30°，OP是角平分线，PC∥OA，PD⊥OA，若PD=1，求PC的长．
如图所示，∠A=60°，CE⊥AB于E，BD⊥AC于D，BD与CE相交于H，HD=1，HE=2，试求BD和CE的长．下列分式的运算正确的是（ ）
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|