题目内容
 如图,CD是平面镜,光线从A点出发经CD上点E反射照到B点,若入射角为α,AC⊥CD,BD⊥CD,且AC=3,BD=6,CD=12,则tanα值为( )
如图,CD是平面镜,光线从A点出发经CD上点E反射照到B点,若入射角为α,AC⊥CD,BD⊥CD,且AC=3,BD=6,CD=12,则tanα值为( )分析:利用入射角等于反射角得到∠CEA=∠DEB=90°-α,易证得Rt△ACE∽Rt△BDE,则AC:BD=CE:ED,即3:6=CE:(12-CE),可求出CE的长,在Rt△ACE中,∠A=α,
然后根据正切的定义即可计算出tanα的值.
然后根据正切的定义即可计算出tanα的值.
解答:解:∵从A点出发经CD上点E反射照到B点,
∴∠CEA=∠DEB=90°-α,
又∵AC⊥CD,BD⊥CD,
∴∠ACE=∠EDB=90°,
∴Rt△ACE∽Rt△BDE,
∴AC:BD=CE:ED,
而AC=3,BD=6,CD=12,
∴3:6=CE:(12-CE),即12-CE=2CE,
∴CE=4,
∵∠A=α,
∴tanα=tanA=
=
.
故选B.
∴∠CEA=∠DEB=90°-α,
又∵AC⊥CD,BD⊥CD,
∴∠ACE=∠EDB=90°,
∴Rt△ACE∽Rt△BDE,
∴AC:BD=CE:ED,
而AC=3,BD=6,CD=12,
∴3:6=CE:(12-CE),即12-CE=2CE,
∴CE=4,
∵∠A=α,
∴tanα=tanA=
| CE |
| AC |
| 4 |
| 3 |
故选B.
点评:本题考查了正切的定义:在直角三角形中,一个锐角的对边与邻边的比叫这个角的正切.也考查了垂线的性质与相似三角形的判定与性质.

练习册系列答案
相关题目
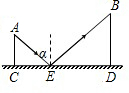 如图,CD是平面镜,光线从A出发经CD上点E发射后照射到B点.若入射角为α,AC⊥CD,BD⊥CD,垂足分别为C、D,且AC=3,BD=6,CD=11,求tanα的值.
如图,CD是平面镜,光线从A出发经CD上点E发射后照射到B点.若入射角为α,AC⊥CD,BD⊥CD,垂足分别为C、D,且AC=3,BD=6,CD=11,求tanα的值. 如图,CD是平面镜,光线从A点出发经CD上点E反射后照射到B点,若入射角为α(入射角等于反射角),
如图,CD是平面镜,光线从A点出发经CD上点E反射后照射到B点,若入射角为α(入射角等于反射角),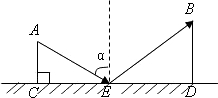 如图,CD是平面镜,光线从A点出发经CD上点E反射后照射到B点,若入射角α(入射角等于反射角),AC⊥CD,BD⊥CD,垂足分别为C、D,且AC=3,BD=6,CD=11,则tanα=
如图,CD是平面镜,光线从A点出发经CD上点E反射后照射到B点,若入射角α(入射角等于反射角),AC⊥CD,BD⊥CD,垂足分别为C、D,且AC=3,BD=6,CD=11,则tanα=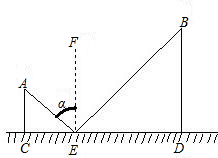 如图,CD是平面镜,光线从A点出发经CD上点E反射照到B点,若入射角为α,AC⊥CD,BD⊥CD,且AC=3,BD=6,CD=12,则tanα值为
如图,CD是平面镜,光线从A点出发经CD上点E反射照到B点,若入射角为α,AC⊥CD,BD⊥CD,且AC=3,BD=6,CD=12,则tanα值为