题目内容
 如图,CD是平面镜,光线从A点出发经CD上点E反射后照射到B点,若入射角为α(入射角等于反射角),
如图,CD是平面镜,光线从A点出发经CD上点E反射后照射到B点,若入射角为α(入射角等于反射角),AC⊥CD,BD⊥CD,垂足分别为C、D,且AC=3,BD=6,CD=12,则sinα的值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:由于AC⊥CD,BD⊥CD,所以AC∥BD,所以△ACE∽△BDE,所以得到
=
=
,∴DE=2CE,又CD=12,由此可以求出CE,再根据已知条件可以求出sinα.
| AC |
| BD |
| CE |
| DE |
| 1 |
| 2 |
解答: 解:∵AC⊥CD,BD⊥CD,
解:∵AC⊥CD,BD⊥CD,
∴∠C=∠D=90°,
∵∠AEC=∠BED,
∴△ACE∽△BDE,
∴
=
=
=
,
∴DE=2CE,
又∵CD=12,
∴CE=4,
∴AE=5,
∴sinα=
=
,
故选:D.
 解:∵AC⊥CD,BD⊥CD,
解:∵AC⊥CD,BD⊥CD,∴∠C=∠D=90°,
∵∠AEC=∠BED,
∴△ACE∽△BDE,
∴
| AC |
| BD |
| CE |
| DE |
| 3 |
| 6 |
| 1 |
| 2 |
∴DE=2CE,
又∵CD=12,
∴CE=4,
∴AE=5,
∴sinα=
| CE |
| AE |
| 4 |
| 5 |
故选:D.
点评:此题主要考查了相似三角形的应用,解此题的关键是把实际问题转化为数学问题,把实际问题抽象到解直角三角形中,利用三角函数解题.

练习册系列答案
相关题目
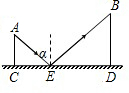 如图,CD是平面镜,光线从A出发经CD上点E发射后照射到B点.若入射角为α,AC⊥CD,BD⊥CD,垂足分别为C、D,且AC=3,BD=6,CD=11,求tanα的值.
如图,CD是平面镜,光线从A出发经CD上点E发射后照射到B点.若入射角为α,AC⊥CD,BD⊥CD,垂足分别为C、D,且AC=3,BD=6,CD=11,求tanα的值.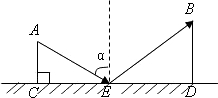 如图,CD是平面镜,光线从A点出发经CD上点E反射后照射到B点,若入射角α(入射角等于反射角),AC⊥CD,BD⊥CD,垂足分别为C、D,且AC=3,BD=6,CD=11,则tanα=
如图,CD是平面镜,光线从A点出发经CD上点E反射后照射到B点,若入射角α(入射角等于反射角),AC⊥CD,BD⊥CD,垂足分别为C、D,且AC=3,BD=6,CD=11,则tanα=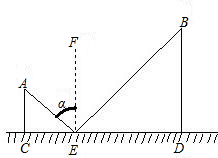 如图,CD是平面镜,光线从A点出发经CD上点E反射照到B点,若入射角为α,AC⊥CD,BD⊥CD,且AC=3,BD=6,CD=12,则tanα值为
如图,CD是平面镜,光线从A点出发经CD上点E反射照到B点,若入射角为α,AC⊥CD,BD⊥CD,且AC=3,BD=6,CD=12,则tanα值为 如图,CD是平面镜,光线从A点出发经CD上点E反射照到B点,若入射角为α,AC⊥CD,BD⊥CD,且AC=3,BD=6,CD=12,则tanα值为( )
如图,CD是平面镜,光线从A点出发经CD上点E反射照到B点,若入射角为α,AC⊥CD,BD⊥CD,且AC=3,BD=6,CD=12,则tanα值为( )