题目内容
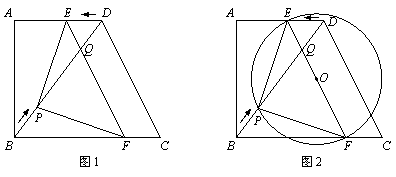
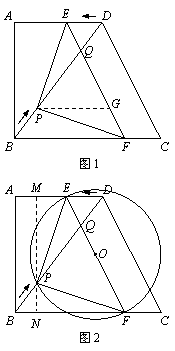
如图1,在直角梯形ABCD中,AD∥BC,∠A=90°,AD=9,AB=12,BC=15.动点P从点B出发,沿BD向点D匀速运动;线段EF从DC出发,沿DA向点A匀速运动,且与BD交于点Q,连接PE、PF.若P、Q两点同时出发,速度均为1个单位∕秒,当P、Q两点相遇时,整个运动停止.设运动时间为t(s).
(1)当PE∥AB时,求t的值;
(2)设△PEF的面积为S,求S关于t的函数关系式;
(3)如图2,当△PEF的外接圆圆心O恰好在EF的中点时,求t的值.
 |
(1)当PE∥AB时,∠DEP=90º,AD=AE+ED=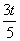 +t=9,…………………(2分)
+t=9,…………………(2分)
解得t=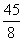 ……………………………………………… (3分)
……………………………………………… (3分)
(2)如图1,过点P作BC的平行线,交EF于G
易得BD=15=BC,………………………(4分)
于是DQ=DE=t,PG=PQ=15-2t……(5分)
∴S=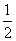 PG•AB=
PG•AB=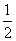 ×12(15-2t)=90-12t…(6分)
×12(15-2t)=90-12t…(6分)
(3)如图2,过点P作BC的垂线,交AD于M,交BC
于N,若△PEF的外接圆圆心O恰好在EF的中点,
即EF为直径,于是∠EPF=90º,易证△EMP∽△PNF…(7分)
从而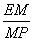 =
=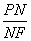 ,可得
,可得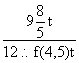 =
=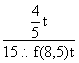 ………(8分)
………(8分)
解得t=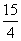 或
或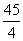 ……………………………(9分)
……………………………(9分)
注意到2t≤15,取t=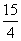 …………………(10分)
…………………(10分)
 |

练习册系列答案
相关题目

 AB,作PF⊥AB,垂足为点F,过点N作NG⊥HK,垂足为点G
AB,作PF⊥AB,垂足为点F,过点N作NG⊥HK,垂足为点G

 自变量x的取值范围是 ;
自变量x的取值范围是 ; (3)已知点C是抛物线上一点,且△ABC的面积为6,求点C的坐标.
(3)已知点C是抛物线上一点,且△ABC的面积为6,求点C的坐标. B.5、5、6 C. 2、
B.5、5、6 C. 2、 、
、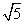 D.
D. 、
、 B、
B、
 D、
D、