题目内容
2.以下各组中不是同类二次根式的是( )| A. | $\sqrt{8}$和$\sqrt{2}$ | B. | $\sqrt{54}$和$\sqrt{108}$ | C. | $\sqrt{8a}$和$\sqrt{32a}$ | D. | $\sqrt{63}$和$\sqrt{112}$ |
分析 根据二次根式的化简计算,把各个二次根式进行化简,根据同类二次根式的概念进行判断即可.
解答 解:$\sqrt{8}$=2$\sqrt{2}$,$\sqrt{8}$与$\sqrt{2}$是同类二次根式;
$\sqrt{54}$=3$\sqrt{6}$,$\sqrt{108}$=6$\sqrt{3}$,$\sqrt{54}$和$\sqrt{108}$不是同类二次根式;
$\sqrt{8a}$=2$\sqrt{2a}$,$\sqrt{32a}$=4$\sqrt{2a}$,$\sqrt{8a}$和$\sqrt{32a}$是同类二次根式;
$\sqrt{63}$=3$\sqrt{7}$,$\sqrt{112}$=4$\sqrt{7}$,$\sqrt{63}$和$\sqrt{112}$是同类二次根式,
故选:B.
点评 本题考查同类二次根式的概念,掌握同类二次根式是化为最简二次根式后,被开方数相同的二次根式称为同类二次根式是解题的关键.

练习册系列答案
相关题目
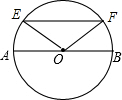 如图,在⊙O中,弦EF∥直径AB,如果$\widehat{AE}$的度数为50°,那么$\widehat{BF}$的度数为50°,∠BOF=50°.
如图,在⊙O中,弦EF∥直径AB,如果$\widehat{AE}$的度数为50°,那么$\widehat{BF}$的度数为50°,∠BOF=50°.