Question

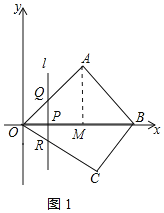
【题目】如图，在平面直角坐标系中，四边形OABC的顶点O是坐标原点，点A在第一象限，点C在第四象限，点B在x轴的正半轴上．∠OAB＝90°且OA＝AB，OB，OC的长分别是二元一次方程组的解（OB＞OC）．

（1）求点A和点B的坐标；

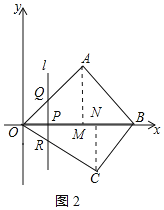
（2）点P是线段OB上的一个动点（点P不与点O，B重合），过点P的直线l与y轴平行，直线l交边OA或边AB于点Q，交边OC或边BC于点R．设点P的横坐标为t，线段QR的长度为m．已知t＝4时，直线l恰好过点C．

①当0＜t＜3时，求m关于t的函数关系式；

②当m＝时，求点P的横坐标t的值．

Answer 1

【答案】（1）点B的坐标为：（6，0），点A的坐标为：（3，3）；（2）①m＝t；②满足条件的点P的横坐标t的值为2或．

【解析】

(1)求出方程的解为，得出OB＝6，OC＝5，点B的坐标为:(6，0)，过点作AM⊥轴于M，则△AOB是等直角三角形，得出OM＝BM＝AM＝OB＝3，即可得出答;

(2)①过点C作CN⊥x轴于N，由题意得出ON＝4，由勾股定理得出CN＝＝3，得出点C的坐标为:(4，-3)，由待定系数法求出直线OC的解析式为:y＝x，得出R(t，t)，由待定系数法直线OA的解析式为:y＝x，得出Q(t，t)，即可得出结果;

②分三种情况:当时，m=, m=, 则t=2;

当3≤t<14时，由得定系数法出直AB的解析式为得出Q()，R)得出方程解方程即可；

当4≤t＜6时，由待定系数法求出直线BC的解析式为:y＝x-9，得Q(t，-t+6)，R(t，t-9)，得出方程，解方程即可.

解：（1）方程组的解为：，

∵OB＞OC，

∴OB＝6，OC＝5，

∴点B的坐标为：（6，0），

过点A作AM⊥x轴于M，如图1所示：

∵∠OAB＝90°且OA＝AB，

∴△AOB是等腰直角三角形，

∴OM＝BM＝AM＝OB＝×6＝3，

∴点A的坐标为：（3，3）；

（2）①过点C作CN⊥x轴于N，如图2所示：

∵t＝4时，直线l恰好过点C，

∴ON＝4，

CN＝＝＝3，

∴点C的坐标为：（4，﹣3），

设直线OC的解析式为：y＝kx，

把C（4，﹣3）代入得：﹣3＝4k，

∴k＝﹣，

∴直线OC的解析式为：y＝﹣x，

∴R（t，﹣t），

设直线OA的解析式为：y＝k′x，

把A（3，3）代入得：3＝3k′，

∴k′＝1，

∴直线OA的解析式为：y＝x，

∴Q（t，t），

∴QR＝t﹣（﹣t）＝t，

即：m＝t；

②分三种情况：

当0＜t＜3时，m＝t，m＝，

则t＝，

解得：t＝2；

当3≤t＜4时，设直线AB的解析式为：y＝px+q，

把A（3，3）、B（6，0）代入得，

解得：，

∴直线AB的解析式为：y＝﹣x+6，

∴Q（t，﹣t+6），R（t，﹣t），

∴m＝﹣t+6﹣（﹣t）＝﹣t+6，

∵m＝，

∴﹣t+6＝，

解得：t＝10＞6（不合题意舍去）；

当4≤t＜6时，设直线BC的解析式为：y＝ax+b，

把B（6，0）、C（4，﹣3）代入得，

解得：，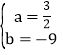

∴直线BC的解析式为：y＝x﹣9，

∴Q（t，﹣t+6），R（t， t﹣9），

∴m＝﹣t+6﹣（t﹣9）＝﹣t+15，

∵m＝，

∴﹣t+15＝，

解得：t＝；

综上所述，满足条件的点P的横坐标t的值为2或．