题目内容
分解因式:
(1)4x3+8x2-4x;
(2)4a2-25b2;
(3)m2-9-2mn+n2;
(4)(a-1)2+5(1-a)+4.
(1)4x3+8x2-4x;
(2)4a2-25b2;
(3)m2-9-2mn+n2;
(4)(a-1)2+5(1-a)+4.
考点:提公因式法与公式法的综合运用
专题:
分析:(1)直接提取公因式4x即可;
(2)利用平方差进行分解即可;
(3)首先分组,把m2-2mn+n2利用完全平方公式分解,再利用平方差进行二次分解;
(4)把a-1看整体,利用十字相乘法分解因式.
(2)利用平方差进行分解即可;
(3)首先分组,把m2-2mn+n2利用完全平方公式分解,再利用平方差进行二次分解;
(4)把a-1看整体,利用十字相乘法分解因式.
解答:解:(1)原式=4x(x2+2x-1);
(2)原式=(2a+5b)(2a-5b);
(3)原式=(m-n)2-9=(m-n-3)(m+n+3);
(4)原式=(a-1-4)(a-1-1)=(a-5)(a-2).
(2)原式=(2a+5b)(2a-5b);
(3)原式=(m-n)2-9=(m-n-3)(m+n+3);
(4)原式=(a-1-4)(a-1-1)=(a-5)(a-2).
点评:本题考查了用提公因式法和公式法进行因式分解,一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解,同时因式分解要彻底,直到不能分解为止.

练习册系列答案
 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
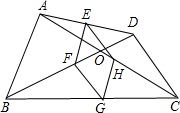 已知:如图,四边形ABCD中,对角线相交于点O、E、F、G、H分别是AD、BD、BC、AC的中点.
已知:如图,四边形ABCD中,对角线相交于点O、E、F、G、H分别是AD、BD、BC、AC的中点. 如图,四边形ABCD是菱形,对角线AC=24,BD=10,过O作OH⊥AB,垂足为H.
如图,四边形ABCD是菱形,对角线AC=24,BD=10,过O作OH⊥AB,垂足为H. 如图,方格纸中每个小正方形的边长为1,△ABC的顶点均在格点上.根据下列要求,利用直尺画图(不写作法):
如图,方格纸中每个小正方形的边长为1,△ABC的顶点均在格点上.根据下列要求,利用直尺画图(不写作法): 如图,直角三角形ABC中,∠C=90°,若AC=3cm,BC=4cm,AB=5cm,则点C到AB的最短距离等于
如图,直角三角形ABC中,∠C=90°,若AC=3cm,BC=4cm,AB=5cm,则点C到AB的最短距离等于