题目内容
如图，四边形ABCD中，∠A=∠C=90°，∠D=60°，AD=5| 3 |
考点：勾股定理,含30度角的直角三角形
专题：
分析：延长DC交AB的延长线与点E，根据直角三角形的性质即可得出DE及AE的长，故可得出BE的长，在由∠C=90°得出BC的长，根据勾股定理求出CE的长，进而可得出结论．
解答：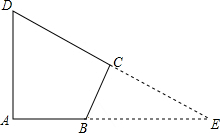
解：延长DC交AB的延长线与点E，
在△ADE中，
∵∠A=90°，∠D=60°，
∴∠E=30°．
∵AD=5
，AB=3，
∴DE=2AD=10
，AE=
=
=15，
∴BE=AE-AB=15-3=12．
∵∠C=90°，∠E=30°，
∴BC=
BE=6．
在Rt△BCE中，CE=
=
=6
，
∴DC=DE-CE=10
-6
=4
．
解：延长DC交AB的延长线与点E，在△ADE中，
∵∠A=90°，∠D=60°，
∴∠E=30°．
∵AD=5
| 3 |
∴DE=2AD=10
| 3 |
| AD |
| tan30° |
5
| ||||
|
∴BE=AE-AB=15-3=12．
∵∠C=90°，∠E=30°，
∴BC=
| 1 |
| 2 |
在Rt△BCE中，CE=
| BE2-BC2 |
| 122-62 |
| 3 |
∴DC=DE-CE=10
| 3 |
| 3 |
| 3 |
点评：本题考查的是勾股定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
练习册系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
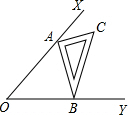如图，∠XOY=45°，一把直角三角尺△ABC的两个顶点A、B分别在OX，OY上移动，其中AB=10，则点O到顶点A的距离的最大值为
如图，在太阳光下同一时刻有两根木棒AB、CD在同一平面上直立着，其中AB这根木棒的影子是BE．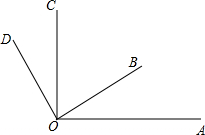
如图，已知∠AOC与∠BOD都是直角，∠BOC=59°