题目内容

6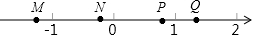．如图，若$\sqrt{{a}^{2}}$=-a，且a＜$\frac{1}{a}$，数a对应于数轴上M、N、P、Q四个点中的一个，则这个点是（　　）
A．点MB．点NC．点PD．点Q

分析 根据二次根式的性质、实数的性质求出a的范围，结合数轴解答即可．

解答 解：∵$\sqrt{{a}^{2}}$=-a，
∴a≤0，
∵a＜$\frac{1}{a}$，
∴a＜-1，
∴数a对应于数轴上M点，
故选：A．

点评 本题考查的是二次根式的化简、实数与数轴，掌握二次根式的性质、实数的大小比较法则是解题的关键．

练习册系列答案
相关题目
16．数a、b、c在数轴上对应的位置如图所示，化简|a+c|-|c+b|+|a-b|．
17．已知抛物线y=-x2+bx+c与x轴交于点A（1，0），B（3，0），与y轴交于点C．
（1）求抛物线的解析式；
（2）设点P在该抛物线上滑动，则满足S△PAB=1的点P有几个？求出所有点P的坐标；
（3）在该抛物线的对称轴上存在点M，使得△MAC的周长最小，求出这个点M的坐标．
14．关于x的两个不等式：①$\frac{a+2x}{3}$＜1与②2（x-2）＞3x-6．
（1）若两个不等式的解集相同，求a的值；
（2）若不等式①的解与不等式②的正整数解之和小于4，求a的取值范围．
1．已知抛物线y=ax2+x+c与x轴交于点A（1，0），B，与y轴交于点C（0，-$\frac{3}{2}$），抛物线的顶点为D，
（1）求抛物线的解析式及点B，D的坐标；
（2）设点P为抛物线上的一点，若△PBC为直角三角形，求点P的坐标；
（3）若点Q为x轴上一点，当△OCD与△BCQ相似时，求点Q的坐标．
11．求满足下列条件的二次函数的解析式．
（1）图象经过A（0，3），B（1，4），C（-1，0）；
（2）图象经过A（-1，0），B（3，0），函数有最小值-12；
（3）图象顶点坐标为A（-2，-3），且经过点（-3，1）．
18．若$\sqrt{{a}^{2}}$=-a，则a≤0．
16．如图，AC∥BE，则（　　）
A．∠C=∠ABEB．∠A=∠EBDC．∠C=∠ABCD．∠A=∠ABE
17．如图，直线l⊥x轴于点P，且与反比例函数y1=$\frac{5}{x}$（x＞0）及y2=$\frac{1}{x}$（x＞0）的图象分别交于点A，B，连结OA，OB，则△OAB的面积为=2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网