题目内容
19. 如图所示,∠A=60°,BC为⊙O的直径,则DE:BC=1:2.
如图所示,∠A=60°,BC为⊙O的直径,则DE:BC=1:2.
分析 连接DC和BE相较于点F,由圆周角定理易证△DEF∽△BCF,由相似三角形的性质可得DE:BC=DF:BF,由已知条件∠A=60°可得∠DFB=30°,再由30°角的正弦值即可求出DF:BF=1:2,进而得到DE:BC的值.
解答 解:
连接DC和BE相较于点F,
∵BC是圆的直径,
∴∠BDC=∠BEC=90°,
∴∠AEB=90°,
∵∠A=60°,
∴∠ABE=30°,
∴DF:BF=1:2,
∵∠EDF=∠FBC,∠DEB=∠BCF,
∴△DEF∽△BCF,
∴DE:BC=DF:BF=1:2,
故答案为1:2.
点评 本题考查了相似三角形的判断和性质以及圆周角定理的运用,题目条件短小而精悍,但隐藏的数学知识点却非常丰富,是一道非常不错的中考试题,熟记圆周角定理是解题的关键.

练习册系列答案
相关题目
7. 已知线段AB=4cm,过点B作BC⊥AB,且BC=2cm,连结AC,以C为圆心,CB为半径作弧,交AC于D;以A为圆心,AD为半径作弧,交AB于P,量一量线段AP的长,约为( )
已知线段AB=4cm,过点B作BC⊥AB,且BC=2cm,连结AC,以C为圆心,CB为半径作弧,交AC于D;以A为圆心,AD为半径作弧,交AB于P,量一量线段AP的长,约为( )
 已知线段AB=4cm,过点B作BC⊥AB,且BC=2cm,连结AC,以C为圆心,CB为半径作弧,交AC于D;以A为圆心,AD为半径作弧,交AB于P,量一量线段AP的长,约为( )
已知线段AB=4cm,过点B作BC⊥AB,且BC=2cm,连结AC,以C为圆心,CB为半径作弧,交AC于D;以A为圆心,AD为半径作弧,交AB于P,量一量线段AP的长,约为( )| A. | 2cm | B. | 2.5cm | C. | 3cm | D. | 3.5cm |
14.将四根长度相等的铁丝首尾顺次相接,连成四边形ABCD,转动这个四边形可以使它的形状改变,当∠B=60°时,如图(1),AC=$\sqrt{2}$;当∠B=90°时,如图(2),此时AC的长为( )
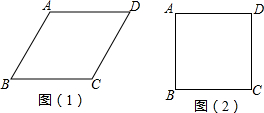
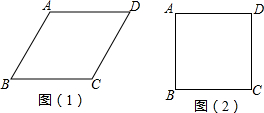
| A. | $2\sqrt{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
