题目内容

3．下列计算正确的是（　　）
A．x+x2=x3B．2x+3x=5x2C．（x2）3=x5D．x5÷x3=x2

分析 根据合并同类项法则；幂的乘方，底数不变指数相乘；同底数幂相除，底数不变指数相减，对各选项分析判断后利用排除法求解．

解答 解：A、x+x2≠x3，此选项错误；
B、2x+3x=5x，此选项错误；
C、（x2）3=x6，此选项错误；
D、x5÷x3=x2，此选项正确；
故选D．

点评 本题考查合并同类项、幂的乘方、同底数幂的除法，熟练掌握运算性质和法则是解题的关键．

练习册系列答案
相关题目
13．要使分式$\frac{x-1}{x+2}$有意义，则x的取值应满足x≠-2．
14．如图，AC⊥BC，直线AM∥CB，点P在线段AB上，点D为射线AC上一动点，连结PD，射线PE⊥PD交直线AM于点E．已知BP=$\sqrt{2}$，AC=BC=4，
（1）如图1，当点D在线段AC上时，求证：PD=PE；
（2）当BA=BD时，请在图2中画出相应的图形，并求线段AE的长；
（3）如果∠EPD的平分线交射线AC于点G，设AD=x，GD=y，求y关于x的函数解析式，并写出自变量的取值范围．
11．若a=（$\frac{1}{4}$）-1+20160，则a=5．
18．下列各组数中，互为相反数的是（　　）
A．2-3与 23B．（-2）-2与2-2C．33 与（-$\frac{1}{3}$）3D．（-3）-3与（$\frac{1}{3}$）3
8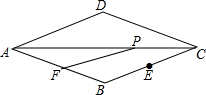．如图，菱形ABCD中，∠D=135°，AD=6，CE=2$\sqrt{2}$，点P是线段AC上一动点，点F是线段AB上一动点，则PE+PF的最小值是（　　）
A．3B．6C．2$\sqrt{5}$D．3$\sqrt{2}$
15．下列计算正确的是（　　）
A．4$\sqrt{3}$-3$\sqrt{3}$=1B．$\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$C．2$\sqrt{\frac{1}{2}}$=$\sqrt{2}$D．$\sqrt{\frac{1}{3}}$•$\sqrt{27}$=$\frac{\sqrt{3}}{3}$
12．已知8x=2，8y=5，则8x+y=10．
13．把多项式2x3y-x2y2-6x2y分解因式时，应提取的公因式为（　　）
A．x2yB．xy2C．2x3yD．6x2y

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网