题目内容
 26、如图,∠AOB=90°,将三角尺的直角顶点落在∠AOB的平分线OC的任意一点P上,使三角尺的两条直角边与∠AOB的两边分别相交于点E、F.
26、如图,∠AOB=90°,将三角尺的直角顶点落在∠AOB的平分线OC的任意一点P上,使三角尺的两条直角边与∠AOB的两边分别相交于点E、F.(1)证明:PE=PF;
(2)若OP=10,试探索四边形PEOF的面积为定值,并求出这个定值.
分析:(1)如果过点P作PM⊥OA于M,PN⊥OB于N.首先利用角平分线的性质得出PM=PN,然后由ASA证出△PME≌△PNF,从而得出PE=PF;
(2)首先证明四边形ONPM是正方形,然后由(1)知△PME≌△PNF,则四边形PEOF的面积=正方形ONPM的面积,又正方形ONPM的对角线OP=10是一个定值,从而得出四边形PEOF的面积为定值,并求出结果.
(2)首先证明四边形ONPM是正方形,然后由(1)知△PME≌△PNF,则四边形PEOF的面积=正方形ONPM的面积,又正方形ONPM的对角线OP=10是一个定值,从而得出四边形PEOF的面积为定值,并求出结果.
解答: 解:(1)过点P作PM⊥OA于M,PN⊥OB于N.
解:(1)过点P作PM⊥OA于M,PN⊥OB于N.
又∵P为∠AOB的平分线OC上的任意一点,
∴PM=PN.
在△PME与△PNF中,∠EMP=∠FNP=90°,PM=PN,∠EPM=∠FPN=90°-∠EPN,
∴△PME≌△PNF,
∴PE=PF;
(2)∵∠OMP=∠MON=∠ONP=90°,
∴四边形ONPM是矩形,
∵PM=PN,
∴矩形ONPM是正方形.
由(1)知△PME≌△PNF,
∴四边形PEOF的面积=正方形ONPM的面积.
又∵OP=10,
∴正方形ONPM的面积=10×10÷2=50,
∴四边形PEOF的面积=50.
 解:(1)过点P作PM⊥OA于M,PN⊥OB于N.
解:(1)过点P作PM⊥OA于M,PN⊥OB于N.又∵P为∠AOB的平分线OC上的任意一点,
∴PM=PN.
在△PME与△PNF中,∠EMP=∠FNP=90°,PM=PN,∠EPM=∠FPN=90°-∠EPN,
∴△PME≌△PNF,
∴PE=PF;
(2)∵∠OMP=∠MON=∠ONP=90°,
∴四边形ONPM是矩形,
∵PM=PN,
∴矩形ONPM是正方形.
由(1)知△PME≌△PNF,
∴四边形PEOF的面积=正方形ONPM的面积.
又∵OP=10,
∴正方形ONPM的面积=10×10÷2=50,
∴四边形PEOF的面积=50.
点评:本题综合考查了角平分线的性质,全等三角形的判定及面积的计算,难度中等.

练习册系列答案
相关题目
 21、如图,∠AOB=90°,点C、D分别在OA、OB上.
21、如图,∠AOB=90°,点C、D分别在OA、OB上. (2013•泉州)如图,∠AOB=90°,∠BOC=30°,则∠AOC=
(2013•泉州)如图,∠AOB=90°,∠BOC=30°,则∠AOC= 画图、证明:如图,∠AOB=90°,点C、D分别在OA、OB上.
画图、证明:如图,∠AOB=90°,点C、D分别在OA、OB上.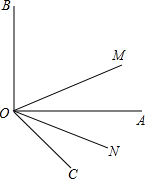 如图,∠AOB=90°,∠AOC为锐角,且ON平分∠AOC,射线OM在∠BON内部.
如图,∠AOB=90°,∠AOC为锐角,且ON平分∠AOC,射线OM在∠BON内部.