题目内容
6.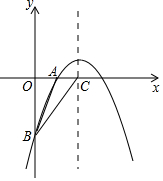 如图,已知二次函数y=-$\frac{1}{2}$x2+bx+c的图象经过A(2,0)、B(0,-6)两点.
如图,已知二次函数y=-$\frac{1}{2}$x2+bx+c的图象经过A(2,0)、B(0,-6)两点.(1)求这个二次函数的解析式.
(2)设该二次函数图象的对称轴与x轴交于点C,连接BA、BC,求△ABC的面积.
(3)根据图象,直接写出函数值y为负数时,自变量x的取值范围.
分析 (1)把A(2,0)、B(0,-6)的坐标代入y=-$\frac{1}{2}$x2+bx+c转化方程组解决即可;
(2)求出点C坐标,根据S△ACB=$\frac{1}{2}$•AC•BO计算即可;
(3)根据A点坐标和对称轴可求出抛物线与x轴的另一交点坐标,可得结果.
解答 解:(1)把A(2,0)、B(0,-6)的坐标代入y=-$\frac{1}{2}$x2+bx+c
得$\left\{\begin{array}{l}{-2+2b+c=0}\\{\;}\\{c=-6}\end{array}\right.$,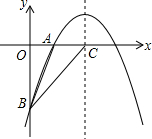
解得$\left\{\begin{array}{l}{b=4}\\{\;}\\{c=-6}\end{array}\right.$,
∴抛物线的解析式为y=-$\frac{1}{2}$x2+4x-6.
(2)∵抛物线的对称轴x=-$\frac{b}{2a}$=-$\frac{4}{-1}$=4,
∴C(4,0),
∵A(2,0)、B(0,-6),
∴AC=2,BO=6,
∴S△ACB=$\frac{1}{2}$•AC•BO=$\frac{1}{2}$×2×6=6;
(3)∵A(2,0),抛物线的对称轴x=-$\frac{b}{2a}$=-$\frac{4}{-1}$=4,
∴抛物线与x轴的另一交点坐标为(6,0)
∴函数值y为负数时,自变量x的取值范围x<2和x>6.
点评 本题考查考查抛物线与x轴的交点、待定系数法、三角形的面积等知识,解题的关键是熟练掌握待定系数法,记住抛物线的对称轴公式,属于中考常考题型.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
18.某体育用品商场为推销某一品牌运动服,先做了市场调查.得到数据如下表:
则P与x的函数关系式为p=-10x+1000,当卖出价格为60元/件时,则销售量为400件.
| 卖出价格x(元/件) | 50 | 51 | 52 | 53 | … |
| 销售量P(件) | 500 | 490 | 480 | 470 | … |
 如图,在平行四边形ABCD中,AB=3cm,BC=5cm,对角线AC,BD相交于点O,则OB的长度取值范围是1<OB<4.
如图,在平行四边形ABCD中,AB=3cm,BC=5cm,对角线AC,BD相交于点O,则OB的长度取值范围是1<OB<4.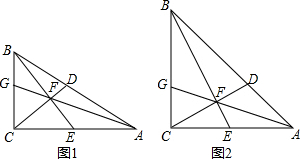
 如图,在?ABCD中,BD是对角线,∠ADB=90°,E、F分别为边AB、CD的中点.
如图,在?ABCD中,BD是对角线,∠ADB=90°,E、F分别为边AB、CD的中点.