题目内容
 在△ABC中,AB=17,BC=21,AC=10,动点P从点C出发,沿着CB运动,速度为每秒3个单位,到达点B时运动停止,设运动时间为t秒,请解答下列问题:
在△ABC中,AB=17,BC=21,AC=10,动点P从点C出发,沿着CB运动,速度为每秒3个单位,到达点B时运动停止,设运动时间为t秒,请解答下列问题:(1)求BC上的高;
(2)当t为何值时,△ACP为等腰三角形?
考点:勾股定理,等腰三角形的判定
专题:动点型
分析:(1)过点A作AD⊥BC于点D,设CD=x,则BD=21-x,再根据勾股定理求出x的值,进而可得出AD的长;
(2)分AC=PC,AP=AC及AP=PC三种情况进行讨论.
(2)分AC=PC,AP=AC及AP=PC三种情况进行讨论.
解答: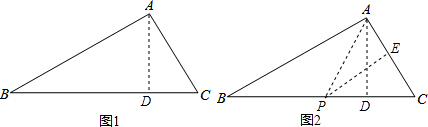 解:(1)过点A作AD⊥BC于点D,设CD=x,则BD=21-x,
解:(1)过点A作AD⊥BC于点D,设CD=x,则BD=21-x,
∵△ABD与△ACD均为直角三角形,
∴AB2-BD2=AC2-CD2,即172-(21-x)2=102-x2,解得x=6,
∴AD=
=
=8;
(2)当AC=PC时,
∵AC=10,
∴AC=PC=10,
∴t=
秒;
当AP=AC时,过点A作AD⊥BC于点D,由(1)知,CD=6,
∴PC=12,
∴t=
=4秒;
当AP=PC时,过点P作PE⊥AC于点E,
∵AC=10,
∴CE=5,
∴
=
,即
=
,解得PC=
,
∴t=
=
秒.
综上所述,t=
秒或4秒或
秒.
 解:(1)过点A作AD⊥BC于点D,设CD=x,则BD=21-x,
解:(1)过点A作AD⊥BC于点D,设CD=x,则BD=21-x,∵△ABD与△ACD均为直角三角形,
∴AB2-BD2=AC2-CD2,即172-(21-x)2=102-x2,解得x=6,
∴AD=
| AC2-BD2 |
| 102-62 |
(2)当AC=PC时,
∵AC=10,
∴AC=PC=10,
∴t=
| 10 |
| 3 |
当AP=AC时,过点A作AD⊥BC于点D,由(1)知,CD=6,
∴PC=12,
∴t=
| 12 |
| 3 |
当AP=PC时,过点P作PE⊥AC于点E,
∵AC=10,
∴CE=5,
∴
| CE |
| PC |
| CD |
| AC |
| 5 |
| PC |
| 6 |
| 10 |
| 25 |
| 3 |
∴t=
| ||
| 3 |
| 25 |
| 9 |
综上所述,t=
| 10 |
| 3 |
| 25 |
| 9 |
点评:本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
相关题目
已知n表示正整数,则
+
=( )
| 1n |
| 2 |
| (-1)n |
| 2 |
| A、0 | B、1 |
| C、0或1 | D、无法确定,随n值的不同而不同 |
下列各式按字母x的降幂排列的是( )
| A、-5x2-x2+2x2 |
| B、ax3-2bx+cx2 |
| C、-x2y-2xy2+y2 |
| D、x2y-3xy2+x3-2y2 |
 已知二次函数y=-x2+2x+k+2与x轴的公共点有两个.求:
已知二次函数y=-x2+2x+k+2与x轴的公共点有两个.求: