题目内容
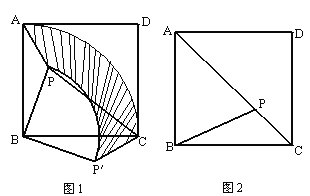
【题目】如图，
，
、
分别是
、
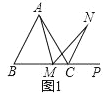
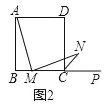
的中点，图①是沿
将
折叠，点
落在
上，图②是绕点将顺时针旋转
.
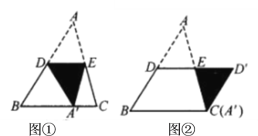
（1）在图①中，判断
和
形状.（填空）_______________________________________
（2）在图②中，判断四边形
的形状，并说明理由.
【答案】（1）
和
均为等腰三角形；（2）四边形
为平行四边形，证明详见解析.
【解析】
根据平行线的性质和折叠的性质解答即可；
（2）由三角形中位线的性质可证
，
，由旋转的性质可知
，从而
，然后根据平行四边形的判定方法可证四边形是平行四边形.
解：（1）和均为等腰三角形.
∵DE∥BC,
∴∠A′DE=∠BA′D, ∠B=∠ADE,
∵∠ADE=∠A′DE,
∴∠B=∠BA′D,
∴BD=A′D，
∴为等腰三角形；
同理可证CE=A′E，即为等腰三角形.
（2）四边形为平行四边形.
理由：
、
分别是
、
的中点，
，.
由旋转的性质可知，
，
四边形是平行四边形.
练习册系列答案
世纪百通期末金卷系列答案
相关题目
