题目内容
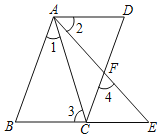
【题目】数学课上，同学们遇到这样一个问题：
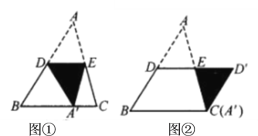
如图1，已知
，
，
、
分别是
与 
的角平分线，请同学们根据题中的条件提出问题，大家一起来解决（本题出现的角均小于平角）
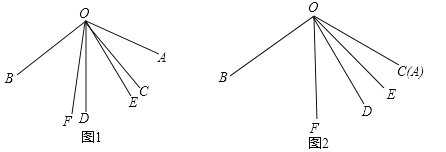
同学们经过思考后，交流了自己的想法：
小强说：“如图2，若
与
重合，且
，
时，可求
的度数．”
小伟说：“在小强提出问題的前提条件下，将
的边从边开始绕点
逆时针
转动
，可求出
的值．”
老师说：“在原題的条件下，借助射线
的不同位置可得出的数量关系．”
(1)请解决小强提出的问题；
(2)在备用图1中，补充完整的图形，并解决小伟提出的问题
(3)在备用图2中，补充完整的图形，并解决老师提出的问题，即求
三者之间的的数量关系．
【答案】（1）45
；（2）
；（3）
、、180、180．
【解析】
（1）根据角平分线定义即可解决小强提出的问题；
（2）在备用图1中，补充完整的图形，根据角平分线定义及角的和差计算即可解决小伟提出的问题；
（3）在备用图2中，补充完整的图形，分四种情况讨论即可解决老师提出的问题，进而求出
三者之间的数量关系．
（1）如图2，
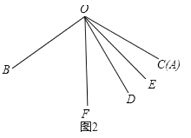
∵∠AOB＝120，OF是∠BOC的角平分线
∴∠FOC＝∠AOB＝60
∵∠COD＝30，OE是∠AOD的角平分线
∴∠EOC＝∠COD＝15
∴∠EOF＝∠FOC∠EOC＝45
答：∠EOF的度数为45；
（2）如图3，
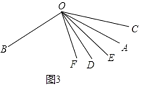
∵OE、OF分别是∠AOD与∠BOC的角平分线，
∴设∠AO＝∠DOE＝∠AOD＝
∠BOF＝∠COF＝∠BOC＝
∴∠BOE＝∠AOB∠AOE＝120
∵∠BOC＝∠AOB＋∠COD∠AOD＝1502
∴∠COF＝75
∴∠DOF＝∠COF∠COD＝7530＝45°
∴∠BOE∠DOF＝（120）（（45）＝75
∵∠COE＝∠COD∠DOE＝30
∴∠EOF＝∠FOC∠COE＝（75）（30）＝45
∴
＝
答：的值为；
（3）∵OE、OF分别是∠AOD与∠BOC的角平分线，
∴设∠AOE＝∠DOE＝∠AOD＝
∠BOF＝∠COF＝∠BOC
∴①如图4，
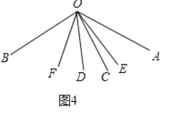
∠AOC＝∠AOD∠COD＝2β
∵∠BOC＝∠AOB∠AOC
＝
（2
）
＝2＋
∴∠FOC＝∠BOC＝ ＋
∵∠COE＝∠DOE∠COD＝
∴∠EOF＝∠FOC＋∠COE
＝
＋＋
＝（）．
②如图5，
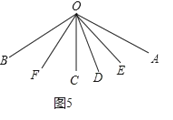
∠AOC＝∠AOD＋∠COD＝2＋
∵∠BOC＝∠AOB∠AOC
＝（2＋）
＝2
∴∠FOC＝∠BOC＝
∵∠COE＝∠DOE＋∠COD＝＋
∴∠EOF＝∠FOC＋∠COE
＝＋＋
＝（＋）．
③如图6，
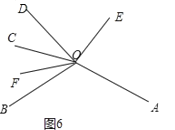
∠AOC＝∠AOD＋∠COD＝2＋
∵∠BOC＝360∠AOB∠AOC
＝360（2＋）
＝3602
∴∠FOC＝∠BOC＝180
∵∠COE＝∠DOE＋∠COD＝＋
∴∠EOF＝∠FOC＋∠COE
＝180＋＋
＝180（）．
④如图7，
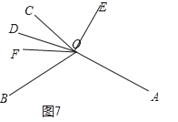
∠AOC＝∠AOD∠COD＝2
∵∠BOC＝360∠AOB∠AOC
＝360（2）
＝3602＋
∴∠FOC＝∠BOC＝180＋
∵∠COE＝∠DOE∠COD＝β
∴∠EOF＝∠FOC＋∠COE
＝180 ＋＋
＝180（＋）．
答：、β、∠EOF三者之间的数量关系为：（
）、（＋）、180（）、180（＋）．
