题目内容
如图,一个二次函数的图象经过点A、C、B三点,点A的坐标为(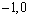 ),点B的坐标为(3,0),点C在y轴的正半轴上,且AB=OC.
),点B的坐标为(3,0),点C在y轴的正半轴上,且AB=OC.
(1)求点C的坐标;
(2)求这个二次函数的解析式,并求出该函数的最大值.
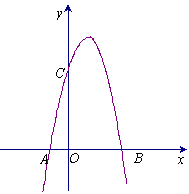
解:(1)∵ A( 1,0)、B(3,0),
1,0)、B(3,0),
∴ AO=1, OB=3,即AB= AO+OB=1+3=4.
∴ OC=4,即点C的坐标为(0,4).
(2)解:设图象经过A、C、B三点的二次函数的解析式为 ,把A、C、B三点的坐标分别代入上式,得
,把A、C、B三点的坐标分别代入上式,得 解得
解得
∴ 所求的二次函数解析式为 .
.
∵ 点A、B的坐标分别为点A 、B
、B ,
,
∴ 线段AB的中点坐标为 ,即抛物线的对称轴为直线
,即抛物线的对称轴为直线 .
.
∵  ,∴ 当
,∴ 当 时,y有最大值
时,y有最大值 .
.
(本题也可设抛物线的顶点式或交点式来解答)

练习册系列答案
相关题目
 的根为 ( )
的根为 ( ) B.x=0 C.x1=2,
B.x=0 C.x1=2, D.x=
D.x= = .
= . 的图象如左图所示,则二次函数y=
的图象如左图所示,则二次函数y= 的图象大致为:
的图象大致为:

 的图象上,则y1,y2,y3的大小关系是 .
的图象上,则y1,y2,y3的大小关系是 . 米.
米.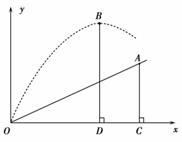
 的结果是( )
的结果是( ) D.
D. 
 ,BD=4,动点P在线段BD上从点B向点D运动,PF⊥AB于点F,四边形PFBG关于BD对称,四边形QEDH与四边形PFBG关于AC对称.设菱形ABCD被这两个四边形盖住部分的面积为S1,未被盖住部分的面积为S2,BP=x.
,BD=4,动点P在线段BD上从点B向点D运动,PF⊥AB于点F,四边形PFBG关于BD对称,四边形QEDH与四边形PFBG关于AC对称.设菱形ABCD被这两个四边形盖住部分的面积为S1,未被盖住部分的面积为S2,BP=x.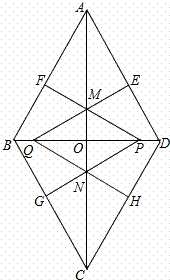
 +1
+1 ﹣
﹣ )×(﹣24)
)×(﹣24)