题目内容
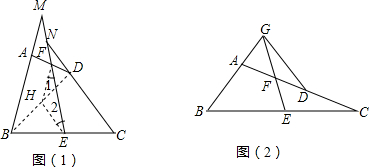
12.【阅读理解】如图,在四边形ABCD中,AB=CD,E、F分别是BC、AD的中点,连结EF并延长,分别与BA、CD的延长线交于点M、N,则∠BEM=∠CNE(不需证明);分析:如图,连结BD,取BD的中点H,连接HE、HF,根据三角形中位线定理,证明HE=HF,从而∠1=∠2,再利用平行线性质,可证得∠BME=∠CNE;
【问题拓展】如图(2),在△ABC中,AC>AB,D点在AC上,AB=CD,E、F分别是BC、AD的中点,连结EF并延长,与BA的延长线交于点G,试判断△AGF的形状,并说明理由.
分析 △AGF是等腰三角形,理由为:连接BD,取BD的中点H,连结HF、HE,则HF是△ABD的中位线,HE是△BDC的中位线,从而判断HE=HF,从而得出∠3=∠AFG,得到△AGF为等腰三角形.
解答 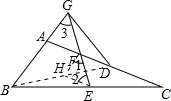 解:△AGF是等腰三角形,理由为:
解:△AGF是等腰三角形,理由为:
证明:如图,连接BD,取BD的中点H,连结HF、HE,
∵F是AD的中点,
∴HF∥AB,HF=$\frac{1}{2}$AB,
∴∠1=∠3,
同理,HE∥CD,HE=$\frac{1}{2}$CD,
∴∠2=∠EFC,
∵∠AFG=∠EFC,
∴∠2=∠AFG,
∵AB=CD,
∴HF=HE,
∴∠1=∠2,
∴∠AFG=∠3,
∴△AGF为等腰三角形.
点评 此题考查了三角形的中位线定理、全等三角形的判定与性质,解答本题的关键是参考题目给出的思路,作出辅助线,有一定难度.

练习册系列答案
相关题目
7.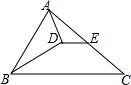 如图,在△ABC中,BD是∠ABC的角平分线,AD⊥BD于D,E是AC的中点,下列结论中不正确的是( )
如图,在△ABC中,BD是∠ABC的角平分线,AD⊥BD于D,E是AC的中点,下列结论中不正确的是( )
 如图,在△ABC中,BD是∠ABC的角平分线,AD⊥BD于D,E是AC的中点,下列结论中不正确的是( )
如图,在△ABC中,BD是∠ABC的角平分线,AD⊥BD于D,E是AC的中点,下列结论中不正确的是( )| A. | ∠BAD=∠C+∠DAE | B. | DE∥BC | C. | DE=$\frac{1}{2}(BC-AB)$ | D. | BD=EC |
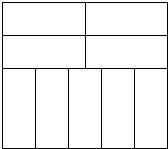 某中学为了提高学生羽毛球水平,准备将一块周长为76m的长方形空地,设计成长、宽分别相等的9块长方形羽毛球场(如图),新建的羽毛球场需要进行装修,已知装修费用为每平方分米1元,问学校要投资多少钱来装修?
某中学为了提高学生羽毛球水平,准备将一块周长为76m的长方形空地,设计成长、宽分别相等的9块长方形羽毛球场(如图),新建的羽毛球场需要进行装修,已知装修费用为每平方分米1元,问学校要投资多少钱来装修?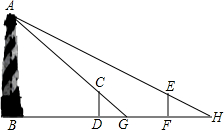 如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB、标杆CD和EF在同一竖直平面内.从标杆CD后退2米到点G处,在G处测得建筑物项端A标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一直线上,则建筑物的高是54米.
如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB、标杆CD和EF在同一竖直平面内.从标杆CD后退2米到点G处,在G处测得建筑物项端A标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一直线上,则建筑物的高是54米.